Question

【题目】已知函数f（x）=|x+1|﹣|2x﹣3|．

（Ⅰ）在图中画出y=f（x）的图象；
（Ⅱ）求不等式|f（x）|＞1的解集．

Answer 1

【答案】解：（Ⅰ）f（x）= ，

由分段函数的图象画法，可得f（x）的图象，如下：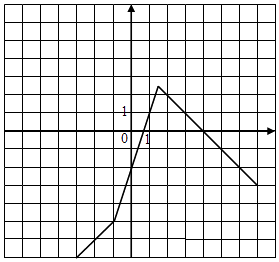

（Ⅱ）由|f（x）|＞1，可得

当x≤﹣1时，|x﹣4|＞1，解得x＞5或x＜3，即有x≤﹣1；

当﹣1＜x＜ 时，|3x﹣2|＞1，解得x＞1或x＜ ，

即有﹣1＜x＜ 或1＜x＜ ；

当x≥ 时，|4﹣x|＞1，解得x＞5或x＜3，即有x＞5或 ≤x＜3．

综上可得，x＜ 或1＜x＜3或x＞5．

则|f（x）|＞1的解集为（﹣∞， ）∪（1，3）∪（5，+∞）．

【解析】（Ⅰ）运用分段函数的形式写出f（x）的解析式，由分段函数的画法，即可得到所求图象；（Ⅱ）分别讨论当x≤﹣1时，当﹣1＜x＜ 时，当x≥ 时，解绝对值不等式，取交集，最后求并集即可得到所求解集．