Question

【题目】如图，在正四棱台中，，分别是的中点.

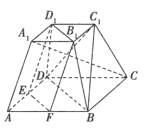
（1）求证：平面平面；

（2）求证：平面.

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

（1）由题设条件，先证明平面，平面，进而得到平面平面；

（2）先由题设条件证明：平面，进而得到平面平面，由，得到平面，故，结合条件即得证.

（1）如下图，连接，交于点，连接，分别交于点，连接.

、分别为、的中点，，

因为平面，平面，所以平面.

又，所以，

又分别是的中点，，

所以，所以.

又，所以，所以四边形为平行四边形，所以.

因为平面，平面，所以平面，

因为，所以平面平面.

（2）连接，，，

因为，所以四边形为平行四边形.

因为，所以四边形为菱形，所以.

因为平面，平面，所以平面平面，

平面平面，因为，平面，

所以平面.

因为平面，所以.

因为，所以平面.