
已知 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,外接圆半径是
,外接圆半径是 ,,且满足条件
,,且满足条件 ,则
,则 的面积的最大值为 ( )
的面积的最大值为 ( )
A. | B. | C. | D. |
C
解析试题分析:由正弦定理可得b=2RsinB=2sinB,代入 得 2sin2A-2sin2C=2sinAsinB-2sin2B,所以sin2A+sin2B-sin2C=sinAsinB,
得 2sin2A-2sin2C=2sinAsinB-2sin2B,所以sin2A+sin2B-sin2C=sinAsinB,
又由正弦定理得:a2+b2-c2=ab,∴cosC=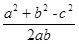
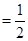 ,又C为三角形的内角,所以C=60°.
,又C为三角形的内角,所以C=60°.
因为ab=a2+b2-c2=a2+b2-(2rsinC)2=a2+b2-3≥2ab-3,所以ab≤3 (当且仅当a=b时,取等号),
所以△ABC面积为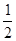 absinC≤
absinC≤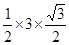 =
= 。
。
考点:本题考查正弦定理;余弦定理;三角形的面积公式;三角函数中的恒等变换;基本不等式的应用。
点评:本题的主要思路是:由ab=a2+b2-3≥2ab-3 求得ab最大值为3,从而求得△ABC面积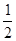 absinC 的最大值.其中求出ab≤3是解题的难点.
absinC 的最大值.其中求出ab≤3是解题的难点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:单选题
函数 的图像为C,如下结论中正确的是( )
的图像为C,如下结论中正确的是( )
A.图像C关于直线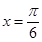 对称
对称
B.图像C关于点 对称
对称
C.函数 在区间
在区间 内是增函数
内是增函数
D.由 的图像向右平移
的图像向右平移 个单位长度可以得到图像C。
个单位长度可以得到图像C。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com