
【题目】如图,在四棱柱![]() 中,底面
中,底面![]() 是等腰梯形,
是等腰梯形,![]() ,顶点
,顶点![]() 在底面
在底面![]() 内的射影恰为点
内的射影恰为点![]() .
.
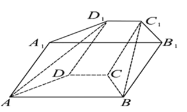
(1)求证:![]() 平面
平面![]() ;
;
(2)若直线![]() 与底面
与底面![]() 所成的角为
所成的角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
【题目】据相关数据统计,2019年底全国已开通![]() 基站13万个,部分省市的政府工作报告将“推进
基站13万个,部分省市的政府工作报告将“推进![]() 通信网络建设”列入2020年的重点工作,今年一月份全国共建基站3万个.
通信网络建设”列入2020年的重点工作,今年一月份全国共建基站3万个.
(1)如果从2月份起,以后的每个月比上一个月多建设2000个,那么,今年底全国共有基站多少万个.(精确到0.1万个)
(2)如果计划今年新建基站60万个,到2022年底全国至少需要800万个,并且,今后新建的数量每年比上一年以等比递增,问2021年和2022年至少各建多少万个オ能完成计划?(精确到1万个)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,
,![]() ,
,![]() 是
是![]() 轴的正半轴上一点,
轴的正半轴上一点,![]() 交椭圆于
交椭圆于![]() ,且
,且![]() ,
,![]() 的内切圆
的内切圆![]() 半径为1.
半径为1.
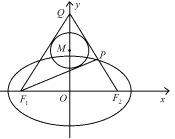
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 点为圆
点为圆![]() 上一点,求
上一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了增强学生的环境意识,某中学随机抽取了50名学生举行了一次环保知识竞赛,本次竞赛的成绩(得分均为整数,满分100分)整理,制成下表:
成绩 |
|
|
|
|
|
|
频数 | 2 | 3 | 14 | 15 | 14 | 4 |
(1)作出被抽查学生成绩的频率分布直方图;
(2)若从成绩在![]() 中选一名学生,从成绩在
中选一名学生,从成绩在![]() 中选出2名学生,共3名学生召开座谈会,求
中选出2名学生,共3名学生召开座谈会,求![]() 组中学生
组中学生![]() 和
和![]() 组中学生
组中学生![]() 同时被选中的概率?
同时被选中的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实常数且
为实常数且![]() ).
).
(Ⅰ)当![]() 时;
时;
①设![]() ,判断函数
,判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
②求证:函数![]() 在
在![]() 上是增函数;
上是增函数;
(Ⅱ)设集合![]() ,若
,若![]() ,求
,求![]() 的取值范围(用
的取值范围(用![]() 表示).
表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市实验中学数学教研组,在高三理科一班进行了一次“采用两种不同方式进行答卷”的考试实验,第一种做卷方式:按从前往后的顺序依次做;第二种做卷方式:先做简单题,再做难题.为了比较这两种做卷方式的效率,选取了![]() 名学生,将他们随机分成两组,每组
名学生,将他们随机分成两组,每组![]() 人.第一组学生用第一种方式,第二组学生用第二种方式,根据学生的考试分数(单位:分)绘制了茎叶图如图所示.
人.第一组学生用第一种方式,第二组学生用第二种方式,根据学生的考试分数(单位:分)绘制了茎叶图如图所示.
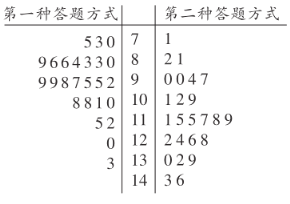
![]() 若
若![]() 分(含
分(含![]() 分)以上为优秀,根据茎叶图估计两种做卷方式的优秀率;
分)以上为优秀,根据茎叶图估计两种做卷方式的优秀率;
![]() 设
设![]() 名学生考试分数的中位数为
名学生考试分数的中位数为![]() ,根据茎叶图填写下面的
,根据茎叶图填写下面的![]() 列联表:
列联表:
超过中位数 | 不超过中位数 | 合计 | |
第一种做卷方式 | |||
第一种做卷方式 | |||
合计 |
根据列联表,能否有![]() 的把握认为两种做卷方式的效率有差异?
的把握认为两种做卷方式的效率有差异?
附: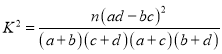 ,
,![]() .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形ABCD是矩形,平面
中,四边形ABCD是矩形,平面![]() 平面ABCD,
平面ABCD,![]() ,E是SB的中点,M是CD上任意一点.
,E是SB的中点,M是CD上任意一点.
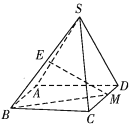
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 平面SAD,求直线BM与平面SAB所成角的正弦值.
平面SAD,求直线BM与平面SAB所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乡镇响应“绿水青山就是金山银山”的号召,因地制宜的将该镇打造成“生态水果特色小镇”.经调研发现:某珍稀水果树的单株产量![]() (单位:千克)与施用肥料
(单位:千克)与施用肥料![]() (单位:千克)满足如下关系:
(单位:千克)满足如下关系: ,肥料成本投入为
,肥料成本投入为![]() 元,其它成本投入(如培育管理、施肥等人工费)
元,其它成本投入(如培育管理、施肥等人工费)![]() 元.已知这种水果的市场售价大约为15元/千克,且销路畅通供不应求.记该水果树的单株利润为
元.已知这种水果的市场售价大约为15元/千克,且销路畅通供不应求.记该水果树的单株利润为![]() (单位:元).
(单位:元).
(Ⅰ)求![]() 的函数关系式;
的函数关系式;
(Ⅱ)当施用肥料为多少千克时,该水果树的单株利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AB⊥侧面BCC1B1,AC=AB1.
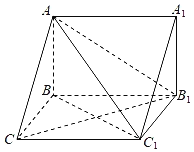
(1)求证:平面ABC1⊥平面AB1C;
(2)若AB=BC=2,∠BCC1=60°,求二面角B﹣AC1﹣B1的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com