
【题目】![]() 大学就业指导中心对该校毕业生就业情况进行跟踪调查,发现不同的学历对就业专业是否为毕业所学专业有影响,就业指导中心从
大学就业指导中心对该校毕业生就业情况进行跟踪调查,发现不同的学历对就业专业是否为毕业所学专业有影响,就业指导中心从![]() 届的毕业生中,抽取了本科和研究生毕业生各
届的毕业生中,抽取了本科和研究生毕业生各![]() 名,得到下表中的数据.
名,得到下表中的数据.
就业专业 毕业学历 | 就业为所学专业 | 就业非所学专业 |
本科 |
|
|
研究生 |
|
|
(1)根据表中的数据,能否在犯错概率不超过![]() 的前提下认为就业专业是否为毕业所学专业与毕业生学历有关;
的前提下认为就业专业是否为毕业所学专业与毕业生学历有关;
(2)为了进一步分析和了解本科毕业生就业的问题,按分层抽样的原则从本科毕业生中抽取一个容量为![]() 的样本,要从
的样本,要从![]() 人中任取
人中任取![]() 人参加座谈,求被选取的
人参加座谈,求被选取的![]() 人中至少有
人中至少有![]() 人就业非毕业所学专业的概率.
人就业非毕业所学专业的概率.
附: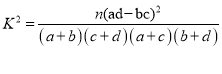 ,
,![]()
|
|
|
|
|
|
|
|
|
|
|
|
 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() .已知
.已知![]() ,其中
,其中![]() 为原点,
为原点, ![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆的方程及离心率![]() 的值;
的值;
(2)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .若
.若![]() ,且
,且![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的右焦点为
的右焦点为![]() ,离心率
,离心率![]() .
.
(1)求椭圆C的标准方程;
(2)已知动直线l过点F,且与椭圆C交于A,B两点,试问x轴上是否存在定点M ,使得![]() 恒成立?若存在,求出点M的坐标,若不存在,请说明理由.
恒成立?若存在,求出点M的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的 500 名志愿者中随机抽取 100 名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是[20,25),[25,30),[30,35),[35,40),[40,45].
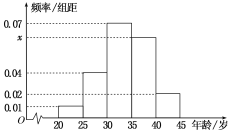
(1)求图中x的值并根据频率分布直方图估计这 500 名志愿者中年龄在[35,40)岁的人数;
(2)在抽出的 100 名志愿者中按年龄采用分层抽样的方法抽取 20 名参加中心广场的宣传活动,再从这 20 名中采用简单随机抽样方法选取 3 名志愿者担任主要负责人.记这 3 名志愿者中“年龄低于 35 岁”的人数为 X,求 X 的分布列及均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校实行选科走班制度,张毅同学的选择是地理生物政治这三科,且生物在B层班级,该校周一上午选科走班的课程安排如下表所示,张毅选择三个科目的课各上一节,另外一节上自习,则他不同的选课方法有__________种
第一节 | 第二节 | 第三节 | 第四节 |
地理1班 | 化学A层3班 | 地理2班 | 化学A层4班 |
生物A层1班 | 化学B层2班 | 生物B层2班 | 历史B层1班 |
物理A层1班 | 生物A层3班 | 物理A层2班 | 生物A层4班 |
物理B层2班 | 生物B层1班 | 物理B层1班 | 物理A层4班 |
政治1班 | 物理A层3班 | 政治2班 | 政治3班 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在盒子里有大小相同,仅颜色不同的乒乓球共10个,其中红球4个,白球3个,蓝球3个。
(Ⅰ)现从中任取出一球确定颜色后放回盒子里,再取下一个球,重复以上操作,最多取3次,过程中如果取出蓝色球则不再取球,求:
①最多取两次就结束的概率;
②整个过程中恰好取到2个白球的概率;
(Ⅱ)若改为从中任取出一球确定颜色后不放回盒子里,再取下一个球。重复以上操作,最多取3次,过程中如果取出蓝色球则不再取球,则设取球的次数为随机变量![]() 求
求![]() 的分布列和数学期望,
的分布列和数学期望,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高三上学期期末数学考试成绩中,随机抽取了![]() 名学生的成绩得到如图所示的频率分布直方图:
名学生的成绩得到如图所示的频率分布直方图:
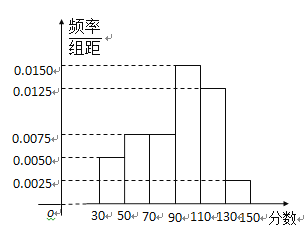
(1)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
(2)若用分层抽样的方法从分数在![]() 和
和![]() 的学生中共抽取
的学生中共抽取![]() 人,该
人,该![]() 人中成绩在
人中成绩在![]() 的有几人?
的有几人?
(3)在(2)中抽取的![]() 人中,随机抽取
人中,随机抽取![]() 人,求分数在
人,求分数在![]() 和
和![]() 各
各![]() 人的概率.
人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com