
已知数列{an}的各项均为正数,前n项的和Sn=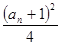
⑴ 求{an}的通项公式;
⑵ 设等比数列{bn}的首项为b,公比为2,前n项的和为Tn.若对任意n∈N*,Sn≤Tn
均成立,求实数b的取值范围.
(1) an=2n-1(n∈N*).(2) b≥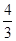 .
.
【解析】
试题分析: (1) a1=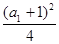 ,解得a1=1.
,解得a1=1.
当n≥2时,由an=Sn-Sn-1=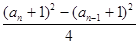 ,
-2
,
-2
得(an-an-1-2)(an+an-1)=0.
又因为an>0,所以an-an-1=2.
因此{an}是首项为1,公差为2的等差数列,
即an=2n-1(n∈N*). 6
(2) 因为Sn=n2,Tn=b(2n-1),
所以Sn≤Tn对任意n∈N*恒成立,
当且仅当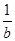 ≤
≤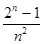 对任意n∈N*均成立.
对任意n∈N*均成立.
令Cn=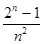 ,因为Cn+1-Cn=
,因为Cn+1-Cn=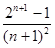 -
-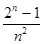 =
=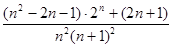 ,
,
所以C1>C2,且当n≥2时,Cn<Cn+1.
因此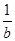 ≤C2=
≤C2=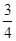 ,即b≥
,即b≥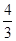 .
.
考点:本题主要考查等差数列的通项公式, “放缩法”证明不等式。
点评:中档题,涉及数列的不等式证明问题,往往需要先求和、再证明。本题(2)通过研究数列的“单调性”,利用“放缩法”,达到证明目的。


科目:高中数学 来源: 题型:
| 2n |
| 3n+1 |
| 3 |
| 5 |
| 11 |
| 17 |
查看答案和解析>>
科目:高中数学 来源:江西省赣县中学2011届高三适应性考试数学理科试题 题型:013
已知数列{an}的通项为an=3n+8,下列各选项中的数为数列{an}中的项的是
8
16
32
36
查看答案和解析>>
科目:高中数学 来源:2011年高三数学复习(第6章 数列):6.1 数列定义与通项(解析版) 题型:解答题
 ,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1)
,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1) (2)
(2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com