
【题目】已知函数f(x)=lnx+ax2-x(x>0,a∈R).
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)求证:当a≤0时,曲线y=f(x)上任意一点处的切线与该曲线只有一个公共点.
【答案】(Ⅰ)见解析;(Ⅱ)见解析
【解析】
(Ⅰ)求出函数的导数,通过讨论a的范围.求出函数的单调区间即可;(Ⅱ)根据函数的单调性以及a的范围证明即可.
(Ⅰ)f′(x)=![]() +2ax-1=
+2ax-1=![]() (x>0),
(x>0),
设g(x)=2ax2-x+1(x>0),
(1)当0<a<![]() 时,g(x)在(0,
时,g(x)在(0,![]() ),(
),(![]() ,+∞)上大于零,
,+∞)上大于零,
在(![]() ,
,![]() )上小于零,
)上小于零,
所以f(x)在(0,![]() ),(
),(![]() ,+∞)上递增,
,+∞)上递增,
在(![]() ,
,![]() )上递减,
)上递减,
(2)当a≥![]() 时,g(x)≥0(当且仅当a=
时,g(x)≥0(当且仅当a=![]() ,x=2时g(x)=0),
,x=2时g(x)=0),
所以f(x)在(0,+∞)上单调递增,
(3)当a=0时,g(x)在(0,1)上大于零,在(1,+∞)上小于零,
所以f(x)在(0,1)上单调递增,在(1,+∞)单调递减,
(4)当a<0时,g(x)在(0,![]() )上大于零,在(
)上大于零,在(![]() ,+∞)上小于零,
,+∞)上小于零,
所以f(x)在(0,![]() )上递增,在(
)上递增,在(![]() ,+∞)上递减;
,+∞)上递减;
(Ⅱ)曲线y=f(x)在点(t,f(t))处的曲线方程为:
y=(![]() +2at-1)(x-t)+lnt+at2-t,
+2at-1)(x-t)+lnt+at2-t,
曲线方程和y=f(x)联立可得:
lnx+ax2-(![]() +2at)x-lnt+at2+1=0,
+2at)x-lnt+at2+1=0,
设h(x)=lnx+ax2-(![]() +2at)x-lnt+at2+1(x>0),
+2at)x-lnt+at2+1(x>0),
h′(x)=![]() ,
,
当a≤0时,在(0,t)h′(x)>0,在(t,+∞)h′(x)<0,
故h(x)在(0,t)递增,在(t,+∞)递减,
又h(t)=0,
故h(x)只有唯一的零点t,
即切线与该曲线只有1个公共点(t,f(t)).


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,公差为
,公差为![]() .
.
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)是否存在![]() ,
,![]() 使
使![]() 成立?若存在,试找出所有满足条件的
成立?若存在,试找出所有满足条件的![]() ,
,![]() 的值,并求出数列
的值,并求出数列![]() 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
(1)任意两个复数都不能比较大小;(2)![]() 为实数
为实数![]() 为实数;(3)虚轴上的点对应的复数都是纯虚数;(4)复数集与复平面内的所有点所成的集合是一一对应的.
为实数;(3)虚轴上的点对应的复数都是纯虚数;(4)复数集与复平面内的所有点所成的集合是一一对应的.
其中正确命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的两个顶点分别为A(2,0),B(2,0),焦点在x轴上,离心率为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)点D为x轴上一点,过D作x轴的垂线交椭圆C于不同的两点M,N,过D作AM的垂线交BN于点E.求证:△BDE与△BDN的面积之比为4:5.
查看答案和解析>>
科目:高中数学 来源: 题型:
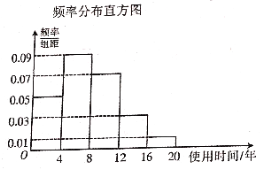
【题目】为了解一款电冰箱的使用时间和市民对这款电冰箱的购买意愿,研究人员对该款电冰箱进行了相应的抽样调查,得到数据的统计图表如下:
购买意愿市民年龄 | 不愿意购买该款电冰箱 | 愿意购买该款电冰箱 | 总计 |
40岁以上 | 600 | 800 | |
40岁以下 | 400 | ||
总计 | 800 |
(1)根据图中的数据,估计该款电冰箱使用时间的中位数;
(2)完善表中数据,并据此判断是否有![]() 的把握认为“愿意购买该款电冰箱“与“市民年龄”有关;
的把握认为“愿意购买该款电冰箱“与“市民年龄”有关;
(3)用频率估计概率,若在该电冰箱的生产线上随机抽取3台,记其中使用时间不低于4年的电冰箱的台数为![]() ,求
,求![]() 的期望.
的期望.
附:![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】住在同一城市的甲、乙两位合伙人,约定在当天下午4:20-5:00间在某个咖啡馆相见商谈合作事宜,他们约好当其中一人先到后最多等对方10分钟,若等不到则可以离去,则这两人能相见的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科技创新公司在第一年年初购买了一台价值昂贵的设备,该设备的第1年的维护费支出为20万元,从第2年到第6年,每年的维修费增加4万元,从第7年开始,每年维修费为上一年的125%.
(1)求第n年该设备的维修费![]() 的表达式;
的表达式;
(2)设![]() ,若
,若![]() 万元,则该设备继续使用,否则须在第n年对设备更新,求在第几年必须对该设备进行更新?
万元,则该设备继续使用,否则须在第n年对设备更新,求在第几年必须对该设备进行更新?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆形纸片的圆心为O,半径为5,该纸片上的等边三角形ABC的中心为O,点D,E,F为圆O上的点,![]() ,
,![]() ,
,![]() 分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起
分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起![]() ,
,![]() ,
,![]() ,使得D,E,F重合于P,得到三棱锥
,使得D,E,F重合于P,得到三棱锥![]() .
.

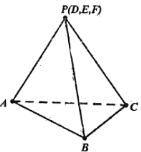
(1)当![]() 时,求三棱锥
时,求三棱锥![]() 的体积;
的体积;
(2)当![]() 的边长变化时,三棱锥
的边长变化时,三棱锥![]() 的侧面和底面所成二面角为
的侧面和底面所成二面角为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com