
已知甲盒内有大小相同的1个红球和3个黑球, 乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为黑球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率;
(Ⅲ)设 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 的分布列和数学期望.
的分布列和数学期望.
(Ⅰ)  .(Ⅱ)
.(Ⅱ)  .(Ⅲ)
.(Ⅲ) 的分布列为:
的分布列为:
0 1 2 3 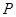




 的数学期望
的数学期望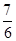 .
.
解析试题分析:(Ⅰ)设“从甲盒内取出的2个球均为黑球”为事件 ,
,
“从乙盒内取出的2个球均为黑球”为事件 .
.
由于事件 相互独立,且
相互独立,且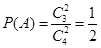 ,
, . 2分
. 2分
故取出的4个球均为黑球的概率为 . 4分
. 4分
(Ⅱ) 设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件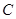 ,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件
,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件 .则
.则  ,
, . 6分
. 6分
由于事件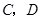 互斥,故取出的4个球中恰有1个红球的概率为
互斥,故取出的4个球中恰有1个红球的概率为 . 8分
. 8分
(Ⅲ) 可能的取值为
可能的取值为 .
.
由(Ⅰ),(Ⅱ)得 ,
, ,
, 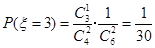 .
.
从而 .
. 的分布列为:
的分布列为:
0 1 2 3 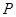




10分 的数学期望
的数学期望 . 12分
. 12分
考点:本题考查了随机变量的概率、分布列及期望
点评:本题考查了随机事件的概率及随机变量的分布列、期望的综合运用,考查了学生的计算能力及解决实际问题的能力,掌握求分布列的步骤及期望公式是解决此类问题的关键


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
哈尔滨市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的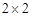 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为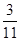 。
。
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合计 | | | 110 |
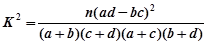 。
。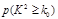 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
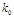 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
从编号为1,2,3,4,5的五个形状大小相同的球中,任取2个球,求:(1)取到的这2个球编号之和为5的概率;(2)取到的这2个球编号之和为奇数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人独立地破译1个密码, 他们能译出密码的概率分别为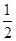 和
和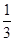 , 求:
, 求:
(1)甲、乙两人至少有一个人破译出密码的概率;
(2)两人都没有破译出密码的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校设计了一个实验考查方案:考生从 道备选题中一次性随机抽取
道备选题中一次性随机抽取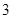 道题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中
道题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中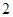 道题的便可通过.已知
道题的便可通过.已知 道备选题中考生甲有
道备选题中考生甲有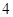 道题能正确完成,
道题能正确完成,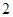 道题不能完成;考生乙每题正确完成的概率都是
道题不能完成;考生乙每题正确完成的概率都是 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)求甲、乙两考生正确完成题数的概率分布列,并计算其数学期望;
(2)请分析比较甲、乙两考生的实验操作能力.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个袋中装有大小相同的黑球和白球共9个,从中任取3个球,记随机变量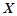 为取出3球中白球的个数,已知
为取出3球中白球的个数,已知 .
.
(Ⅰ)求袋中白球的个数;
(Ⅱ)求随机变量 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了参加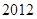 贵州省高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出
贵州省高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出 人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
| 班级 | 高三(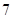 )班 )班 | 高三(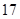 )班 )班 | 高二(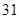 )班 )班 | 高二(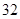 )班 )班 |
| 人数 | 12 | 6 | 9 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
甲,乙,丙三位学生独立地解同一道题,甲做对的概率为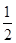 ,乙,丙做对的概率分别为
,乙,丙做对的概率分别为 ,
, (
( >
> ),且三位学生是否做对相互独立.记
),且三位学生是否做对相互独立.记 为这三位学生中做对该题的人数,其分布列为:
为这三位学生中做对该题的人数,其分布列为:
 | 0 | 1 | 2 | 3 |
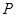 | 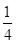 |  | 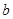 | 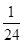 |
 ,
, 的值;
的值; 的数学期望.
的数学期望. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
先后2次抛掷一枚骰子,将得到的点数分别记为a,b.
(1)求直线ax+by+5=0与圆x2+y2=1相切的概率;
(2)将a,b,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com