
【题目】已知函数y=f(x)的导函数y=f′(x)的图象如图所示,则关于函数y=f(x),下列说法正确的是( ) 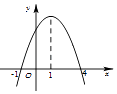
A.在x=﹣1处取得极大值
B.在区间[﹣1,4]上是增函数
C.在x=1处取得极大值
D.在区间[1,+∞)上是减函数
【答案】B
【解析】解:由导函数y=f′(x)的图象,可知f(﹣1)=0,f(4)=0, x∈(﹣∞,﹣1),f′(x)<0,函数是减函数,
x∈(﹣1,4),f′(x)>0,函数是增函数,
x∈(4,+∞),f′(x)<0,函数是减函数,
故选:B.
【考点精析】利用利用导数研究函数的单调性和函数的极值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:高中数学 来源: 题型:
【题目】函数f(x)=x2+ax+3,已知不等式f(x)<0的解集为{x|1<x<3}.
(1)求a;
(2)若不等式f(x)≥m的解集是R,求实数m的取值范围;
(3)若f(x)≥nx对任意的实数x≥1成立,求实数n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|< ![]() )的最小正周期为2 π,最小值为﹣2,且当x=
)的最小正周期为2 π,最小值为﹣2,且当x= ![]() 时,函数取得最大值4. (Ⅰ)求函数 f(x)的解析式;
时,函数取得最大值4. (Ⅰ)求函数 f(x)的解析式;
(Ⅱ)求函数f(x)的单调递增区间;
(Ⅲ)若当x∈[ ![]() ,
, ![]() ]时,方程f(x)=m+1有解,求实数m的取值范围.
]时,方程f(x)=m+1有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直二面角D﹣AB﹣E中,四边形ABCD是边长为2的正方形,AE=EB,点F在CE上,且BF⊥平面ACE; 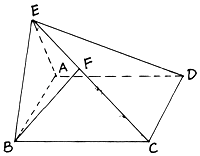
(1)求证:AE⊥平面BCE;
(2)求二面角B﹣AC﹣E的正弦值;
(3)求点D到平面ACE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=x3+ax2+bx+1的导数f′(x)满足f′(1)=2a,f′(2)=﹣b,其中常数a,b∈R. (Ⅰ)求曲线y=f(x)在点(1,f(1))处的切线方程.
(Ⅱ)设g(x)=f′(x)e﹣x . 求函数g(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为R,f(1)=3,对任意x∈R,f′(x)<2,则f(x)<2x+1的解集为( )
A.(1,+∞)
B.(﹣1,1)
C.(﹣∞,1)
D.(﹣∞,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四棱柱ABCD﹣A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC 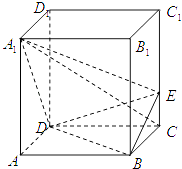
(1)证明:A1C⊥平面BED;
(2)求二面角A1﹣DE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 图象上不同两点
图象上不同两点![]() ,
, ![]() 处切线的斜率分别是
处切线的斜率分别是![]() ,
, ![]() ,规定
,规定![]() (
(![]() 为线段
为线段![]() 的长度)叫做曲线
的长度)叫做曲线![]() 在点
在点![]() 与
与![]() 之间的“弯曲度”,给出以下命题:
之间的“弯曲度”,给出以下命题:
①函数![]() 图象上两点
图象上两点![]() 与
与![]() 的横坐标分别为1和2,则
的横坐标分别为1和2,则![]() ;
;
②存在这样的函数,图象上任意两点之间的“弯曲度”为常数;
③设点![]() ,
, ![]() 是抛物线
是抛物线![]() 上不同的两点,则
上不同的两点,则![]() ;
;
④设曲线![]() (
(![]() 是自然对数的底数)上不同两点
是自然对数的底数)上不同两点![]() ,
, ![]() ,且
,且![]() ,若
,若![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是![]() .
.
其中真命题的序号为__________.(将所有真命题的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com