
定义在D上的函数![]() ,如果满足:
,如果满足:![]() ,
,![]() 常数
常数![]() ,都有
,都有![]() ≤M成立,则称
≤M成立,则称![]() 是D上的有界函数,其中M称为函数的上界.
是D上的有界函数,其中M称为函数的上界.
(Ⅰ)试判断函数![]() 在[1,3]上是不是有界函数?请给出证明;
在[1,3]上是不是有界函数?请给出证明;
(Ⅱ)若已知质点的运动方程为![]() ,要使在
,要使在![]() 上的每一时刻的瞬时速度是以M=1为上界的有界函数,求实数a的取值范围.
上的每一时刻的瞬时速度是以M=1为上界的有界函数,求实数a的取值范围.
科目:高中数学 来源: 题型:

| 48 |
| x |
| b |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如右图所示,定义在D上的函数f(x),如果满足:对?x∈D,常数A,都有f(x)≥A成立,则称函数f(x)在D上有下界,其中A称为函数的下界.(提示:图中的常数A可以是正数,也可以是负数或零)
如右图所示,定义在D上的函数f(x),如果满足:对?x∈D,常数A,都有f(x)≥A成立,则称函数f(x)在D上有下界,其中A称为函数的下界.(提示:图中的常数A可以是正数,也可以是负数或零)| 48 |
| x |
| t+1 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:

| 48 |
| x |
| t+1 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
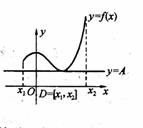 (本题满分12)如右图所示,定义在D上的函数
(本题满分12)如右图所示,定义在D上的函数![]() ,如果满足:对
,如果满足:对![]() ,
,![]() 常数A,都有
常数A,都有![]() 成立,则称函数
成立,则称函数![]() 在D上有下界,其中A称为函数的下界.(提示:图中的常数A可以是正数,也可以是负数或零)
在D上有下界,其中A称为函数的下界.(提示:图中的常数A可以是正数,也可以是负数或零)
(1)试判断函数![]() 在
在![]() 上是否有下界?并说明理由;
上是否有下界?并说明理由;
(2)已知某质点的运动方程为![]() ,要使在
,要使在![]() 上的每一时刻该质点的瞬时速度是以
上的每一时刻该质点的瞬时速度是以![]() 为下界的函数,求实数a的取值范围.
为下界的函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2008-2009学年江苏省扬州中学高三(上)月考数学试卷(解析版) 题型:解答题
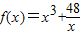 在(0,+∞)上是否有下界?并说明理由;
在(0,+∞)上是否有下界?并说明理由;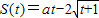 ,要使在t∈[0,+∞)上的每一时刻该质点的瞬时速度是以
,要使在t∈[0,+∞)上的每一时刻该质点的瞬时速度是以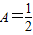 为下界的函数,求实数a的取值范围.
为下界的函数,求实数a的取值范围.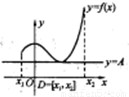
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com