
修建一个面积为 平方米的矩形场地的围墙,要求在前面墙的正中间留一个宽度为2米的出入口,后面墙长度不超过20米,已知后面墙的造价为每米45元,其它墙的造价为每米180元,设后面墙长度为x米,修建此矩形场地围墙的总费用为
平方米的矩形场地的围墙,要求在前面墙的正中间留一个宽度为2米的出入口,后面墙长度不超过20米,已知后面墙的造价为每米45元,其它墙的造价为每米180元,设后面墙长度为x米,修建此矩形场地围墙的总费用为 元.
元.
(1)求 的表达式;
的表达式;
(2)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
(1)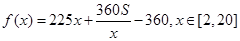 ;(2)若
;(2)若 ,最小总费用为
,最小总费用为 (元).
(元). ,则当
,则当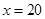 时,最小总费用为
时,最小总费用为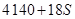 (元). .
(元). .
解析试题分析:(1)根据条件可以将所有墙的长度都用含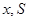 的代数式表示出来,再由墙的造价,即可得到
的代数式表示出来,再由墙的造价,即可得到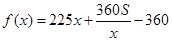 ,又由条件后墙长度不超过20米及前墙留一个宽度为2米的出入口,可知
,又由条件后墙长度不超过20米及前墙留一个宽度为2米的出入口,可知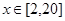 ;(2)由(1)中所求表达式可知,要求最小费用,即求
;(2)由(1)中所求表达式可知,要求最小费用,即求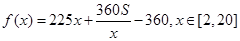 ,而
,而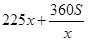 是一个“对钩”函数,需对
是一个“对钩”函数,需对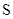 的取值范围分类讨论:①
的取值范围分类讨论:① ,②
,② ,从而利用“对钩”函数的单调性求
,从而利用“对钩”函数的单调性求 的最小值.
的最小值.
(1)画出如下示意图,由矩形的面积为S,可知与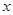 相邻的边长为
相邻的边长为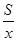 ,∴总费用
,∴总费用 ,
,
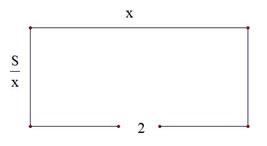
显然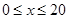 ,∴
,∴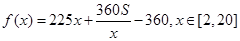 ;
;
(2)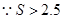 ,则
,则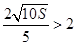 ,可以证明
,可以证明 在
在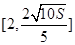 递减,在
递减,在 递增.
递增.
若 ,即
,即 ,则当
,则当 时,最小总费用为
时,最小总费用为 (元).
(元).
若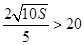 ,即
,即 ,则当
,则当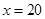 时,
时,
最小总费用为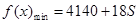 (元).
(元).
考点:1.函数的运用;2.函数单调性求极值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
已知函数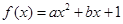 (
( 为实数,
为实数, ),
), ,⑴若
,⑴若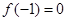 ,且函数
,且函数 的值域为
的值域为 ,求
,求 的表达式;
的表达式;
⑵设 ,且函数
,且函数 为偶函数,判断
为偶函数,判断 是否大0?
是否大0?
⑶设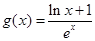 ,当
,当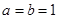 时,证明:对任意实数
时,证明:对任意实数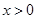 ,
, (其中
(其中 是
是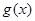 的导函数) .
的导函数) .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 为常数,且
为常数,且 ,函数
,函数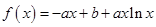 ,
,
( 是自然对数的底数).
是自然对数的底数).
(1)求实数 的值;
的值;
(2)求函数 的单调区间;
的单调区间;
(3)当 时,是否同时存在实数
时,是否同时存在实数 和
和 (
( ),使得对每一个
),使得对每一个 ,直线
,直线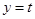 与曲线
与曲线
 都有公共点?若存在,求出最小的实数
都有公共点?若存在,求出最小的实数 和最大的实数
和最大的实数 ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=ax2+1,g(x)=x3+bx,其中a>0,b>0.
(1)若曲线y=f(x)与曲线y=g(x) 在它们的交点P(2,c)处有相同的切线(P为切点),求实数a,b的值;
(2)令h (x)=f(x)+g(x),若函数h(x)的单调减区间为 .
.
①求函数h(x)在区间(-∞,-1]上的最大值M(a);
②若|h(x)|≤3在x∈[-2,0]上恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com