
A、P1=
| ||||||
B、P1=
| ||||||
C、P1=
| ||||||
D、P1=
|
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源:中华一题 高中数学必修3·B版(配套人民教育出版社实验教科书) 人教版 题型:044
写出下列随机试验的基本事件空间及表示下列事件的基本事件的集合.
(1)10件产品中有1件是不合格品,从中任取2件得1件不合格品;
(2)一个口袋中有2个白球、3个黑球、4个红球,从中任取一球,①得白球,②得黑球.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 P2=
P2= P3=
P3=
 P2=
P2= P3=
P3=
 P2=
P2= P3=
P3=
 P2=
P2= P3=
P3=
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.P1=
| B.P1=
| ||||||||||||
C.P1=
| D.P1=
|
查看答案和解析>>
科目:高中数学 来源:《第3章 概率》2013年单元测试卷(解析版) 题型:选择题
 P2=
P2= P3=
P3=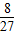
 P2=
P2=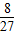 P3=
P3=
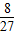 P2=
P2= P3=
P3=
 P2=
P2= P3=
P3=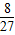
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com