
ЁОЬтФПЁПФГЭЖзЪЙЋЫОМЦЛЎЭЖзЪAЃЌBСНжжН№ШкВњЦЗЃЌИљОнЪаГЁЕїВщгыдЄВтЃЌAВњЦЗЕФРћШѓy1гыЭЖзЪН№ЖюxЕФКЏЪ§ЙиЯЕЮЊy1=18Љ ![]() ЃЌBВњЦЗЕФРћШѓy2гыЭЖзЪН№ЖюxЕФКЏЪ§ЙиЯЕЮЊy2=
ЃЌBВњЦЗЕФРћШѓy2гыЭЖзЪН№ЖюxЕФКЏЪ§ЙиЯЕЮЊy2= ![]() ЃЈзЂЃКРћШѓгыЭЖзЪН№ЖюЕЅЮЛЃКЭђдЊЃЉЃЎ
ЃЈзЂЃКРћШѓгыЭЖзЪН№ЖюЕЅЮЛЃКЭђдЊЃЉЃЎ
ЃЈ1ЃЉИУЙЋЫОвбга100ЭђдЊзЪН№ЃЌВЂШЋВПЭЖШыAЃЌBСНжжВњЦЗжаЃЌЦфжаxЭђдЊзЪН№ЭЖШыAВњЦЗЃЌЪдАбAЃЌBСНжжВњЦЗРћШѓзмКЭБэЪОЮЊxЕФКЏЪ§ЃЌВЂаДГіЖЈвхгђЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌЪдЮЪЃКдѕбљЗжХфет100ЭђдЊзЪН№ЃЌВХФмЪЙЙЋЫОЛёЕУзюДѓРћШѓЃПЦфзюДѓРћШѓЮЊЖрЩйЭђдЊЃП
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКЦфжаxЭђдЊзЪН№ЭЖШыAВњЦЗЃЌдђЪЃгрЕФ100ЉxЃЈЭђдЊЃЉзЪН№ЭЖШыBВњЦЗЃЌ
РћШѓзмКЭfЃЈxЃЉ=18Љ ![]() +
+ ![]() =38Љ
=38Љ ![]() Љ
Љ ![]() ЃЈxЁЪ[0ЃЌ100]ЃЉЃЎ
ЃЈxЁЪ[0ЃЌ100]ЃЉЃЎ
ЃЈ2ЃЉНтЃКЁпfЃЈxЃЉ=40Љ ![]() Љ
Љ ![]() ЃЌxЁЪ[0ЃЌ100]ЃЌ
ЃЌxЁЪ[0ЃЌ100]ЃЌ
ЁргЩЛљБОВЛЕШЪНЕУЃКfЃЈxЃЉЁм40Љ2 ![]() =28ЃЌШЁЕШКХЃЌЕБЧвНіЕБ
=28ЃЌШЁЕШКХЃЌЕБЧвНіЕБ ![]() =
= ![]() ЪБЃЌМДx=20ЃЎ
ЪБЃЌМДx=20ЃЎ
Д№ЃКЗжБ№гУ20ЭђдЊКЭ80ЭђдЊзЪН№ЭЖзЪAЁЂBСНжжН№ШкВњЦЗЃЌПЩвдЪЙЙЋЫОЛёЕУзюДѓРћШѓЃЌзюДѓРћШѓЮЊ28ЭђдЊЃЎ
ЁОНтЮіЁПЃЈ1ЃЉЦфжаxЭђдЊзЪН№ЭЖШыAВњЦЗЃЌдђЪЃгрЕФ100ЉxЃЈЭђдЊЃЉзЪН№ЭЖШыBВњЦЗЃЌИљОнAВњЦЗЕФРћШѓy1гыЭЖзЪН№ЖюxЕФКЏЪ§ЙиЯЕЮЊy1=18Љ ![]() ЃЌBВњЦЗЕФРћШѓy2гыЭЖзЪН№ЖюxЕФКЏЪ§ЙиЯЕЮЊy2=
ЃЌBВњЦЗЕФРћШѓy2гыЭЖзЪН№ЖюxЕФКЏЪ§ЙиЯЕЮЊy2= ![]() ЃЌПЩЕУРћШѓзмКЭЃЛЃЈ2ЃЉfЃЈxЃЉ=40Љ
ЃЌПЩЕУРћШѓзмКЭЃЛЃЈ2ЃЉfЃЈxЃЉ=40Љ ![]() Љ
Љ ![]() ЃЌxЁЪ[0ЃЌ100]ЃЌгЩЛљБОВЛЕШЪНЃЌПЩЕУНсТлЃЎ
ЃЌxЁЪ[0ЃЌ100]ЃЌгЩЛљБОВЛЕШЪНЃЌПЩЕУНсТлЃЎ


 аЁбЇЩњ10ЗжжгПкЫуВтЪд100ЗжЯЕСаД№АИ
аЁбЇЩњ10ЗжжгПкЫуВтЪд100ЗжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕШВюЪ§Са![]() Тњзу
Тњзу![]() ЃЌ
ЃЌ ![]() ЃЎ
ЃЎ
ЃЈ![]() ЃЉЧѓ
ЃЉЧѓ![]() ЕФЭЈЯюЙЋЪНЃЎ
ЕФЭЈЯюЙЋЪНЃЎ
ЃЈ![]() ЃЉЩшЕШБШЪ§Са
ЃЉЩшЕШБШЪ§Са![]() Тњзу
Тњзу![]() ЃЌ
ЃЌ ![]() ЃЌЮЪЃК
ЃЌЮЪЃК ![]() гыЪ§Са
гыЪ§Са![]() ЕФЕкМИЯюЯрЕШЃП
ЕФЕкМИЯюЯрЕШЃП
ЃЈ![]() ЃЉЪдБШНЯ
ЃЉЪдБШНЯ![]() гы
гы![]() ЕФДѓаЁЃЌВЂЫЕУїРэгЩЃЎ
ЕФДѓаЁЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() Й§Еу
Й§Еу![]() ЃЌЦфРыаФТЪЮЊ
ЃЌЦфРыаФТЪЮЊ![]() .
.
ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉжБЯп![]() гы
гы![]() ЯрНЛгк
ЯрНЛгк![]() СНЕуЃЌдк
СНЕуЃЌдк![]() жсЩЯЪЧЗёДцдкЕу
жсЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЮЊе§Ш§НЧаЮЃЌШєДцдкЃЌЧѓжБЯп
ЮЊе§Ш§НЧаЮЃЌШєДцдкЃЌЧѓжБЯп![]() ЕФЗНГЬЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФЗНГЬЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЪЕЪ§МЏRжаЖЈвхвЛжждЫЫуЁАЁбЁБЃЌОпгааджЪЃКЂйЖдШЮвтaЁЂbЁЪRЃЌaЁбb=bЁбaЃЛЂкaЁб0=aЃЛЂлЖдШЮвтaЁЂbЁЪRЃЌЃЈaЁбbЃЉЁбc=ЃЈabЃЉЁбc+ЃЈaЁбcЃЉ+ЃЈbЁбcЃЉЉ2cЃЌдђКЏЪ§fЃЈxЃЉ=xЁб ![]() ЕФзюаЁжЕЪЧЃЈ ЃЉ
ЕФзюаЁжЕЪЧЃЈ ЃЉ
A.2
B.3
C.![]()
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪ§Са{an}ТњзуSn=2nЉanЃЈnЁЪN*ЃЉЃЎ ЃЈЂёЃЉМЦЫуa1 ЃЌ a2 ЃЌ a3 ЃЌ a4 ЃЌ ВЂгЩДЫВТЯыЭЈЯюЙЋЪНanЃЛ
ЃЈЂђЃЉгУЪ§бЇЙщФЩЗЈжЄУїЃЈЂёЃЉжаЕФВТЯыЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖPЉABCDжаЃЌPAЁЭЦНУцABCDЃЌЫФБпаЮABCDЮЊе§ЗНаЮЃЌAB=PA=4ЃЌAЕудкPDЩЯЕФЩфгАЮЊGЕуЃЌEЕудкABЩЯЃЌЦНУцPCEЁЭЦНУцPCDЃЎ 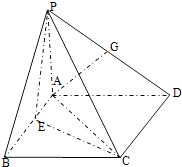
ЃЈ1ЃЉЧѓжЄЃКAGЁЭЦНУцPCDЃЛ
ЃЈ2ЃЉЧѓжБЯпPDгыЦНУцPCEЫљГЩНЧЕФе§ЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаХаЖЯе§ШЗЕФЪЧ ЃЎ ЃЈЬюаДЫљгае§ШЗЕФађКХЃЉ ЂйШєsinx+siny= ![]() ЃЌдђsinyЉcos2xЕФзюДѓжЕЮЊ
ЃЌдђsinyЉcos2xЕФзюДѓжЕЮЊ ![]() ЃЛ
ЃЛ
ЂкКЏЪ§y=sinЃЈ2x+ ![]() ЃЉЕФЕЅЕїдіЧјМфЪЧ[kІаЉ
ЃЉЕФЕЅЕїдіЧјМфЪЧ[kІаЉ ![]() ЃЌkІа+
ЃЌkІа+ ![]() ]ЃЌkЁЪZЃЛ
]ЃЌkЁЪZЃЛ
ЂлКЏЪ§fЃЈxЃЉ= ![]() ЪЧЦцКЏЪ§ЃЛ
ЪЧЦцКЏЪ§ЃЛ
ЂмКЏЪ§y=tan ![]() Љ
Љ ![]() ЕФзюаЁе§жмЦкЪЧІаЃЎ
ЕФзюаЁе§жмЦкЪЧІаЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=2cosxsinЃЈx+ ![]() ЃЉЉ
ЃЉЉ ![]() sin2x+sinxcosxЃЎ
sin2x+sinxcosxЃЎ 
ЃЈ1ЃЉЕБxЁЪ[0ЃЌ ![]() ]ЪБЃЌЧѓfЃЈxЃЉЕФжЕгђЃЛ
]ЪБЃЌЧѓfЃЈxЃЉЕФжЕгђЃЛ
ЃЈ2ЃЉгУЮхЕуЗЈдкЭМжазїГіy=fЃЈxЃЉдкБеЧјМф[Љ ![]() ЃЌ
ЃЌ ![]() ]ЩЯЕФМђЭМЃЛ
]ЩЯЕФМђЭМЃЛ
ЃЈ3ЃЉЫЕУїfЃЈxЃЉЕФЭМЯѓПЩгЩy=sinxЕФЭМЯѓОЙ§дѕбљЕФБфЛЏЕУЕНЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫДйНјбЇЩњЕФШЋУцЗЂеЙЃЌжЃжнЪаФГжабЇжиЪгбЇЩњЩчЭХЮФЛЏНЈЩшЃЌЯжгУЗжВуГщбљЕФЗНЗЈДгЁАЛАОчЩчЁБЃЌЁАДДПЭЩчЁБЃЌЁАбнНВЩчЁБШ§ИіН№ХЦЩчЭХжаГщШЁ6ШЫзщГЩЩчЭХЙмРэаЁзщЃЌгаЙиЪ§ОнМћБэЃЈЕЅЮЛЃКШЫЃЉЃК
ЩчЭХУћГЦ | ГЩдБШЫЪ§ | ГщШЁШЫЪ§ |
ЛАОчЩч | 50 | a |
ДДПЭЩч | 150 | b |
бнНВЩч | 100 | c |
ЃЈ1ЃЉЧѓaЃЌbЃЌcЕФжЕЃЛ
ЃЈ2ЃЉШєДгЁАЛАОчЩчЁБЃЌЁАДДПЭЩчЁБЃЌЁАбнНВЩчЁБвбГщШЁЕФ6ШЫжаШЮвтГщШЁ2ШЫЕЃШЮЙмРэаЁзщзщГЄЃЌЧѓет2ШЫРДздВЛЭЌЩчЭХЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com