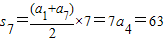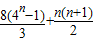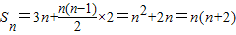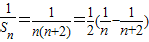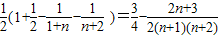Question

设{a_n}是等差数列，其前n项和为S_n，已知S₇=63，a₄+a₅+a₆=33，
（1）写出数列{a_n}的通项公式；
（2） 求数列b_n=2^an+n，求数列{b_n}的前n项和Tn；
（3） 求证：+++…+＜

Answer 1

【答案】分析：（1）利用等差数列的性质若p+q=m+n，a_n+a_m=a_p+a_q，由S₇=63，a₄+a₅+a₆=33，可得a₄，a₅，进一步可求公差d的值，从而求出a
（2）由（1）中所求a_n可得b_{n=2²ⁿ⁺¹+n}，分别用等差数列及等比数列的前n和公式，利用分组求和求Tn
（3）利用裂项求和
解答：解：（1）∵
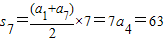
∴a₄=9，又a₄+a₅+a₆=33，3a₅=33，则a₅=11
 公差d=2，a_n=2n+1；
（2）∵b_n=2^an+n=2²ⁿ⁺¹+n
∴T_n=b₁+b₂+…+b_n=（2³+1）+（2⁵+2）+••+（2²ⁿ⁺¹+n）
=（2³+2⁵+…+2²ⁿ⁺¹）+（1+2+…+n）
=
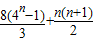
 （3）由等差数列的前n项和公式可得，
∴
∴
=
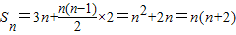
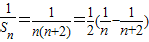
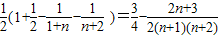
点评：利用等差数列的性质求相关量是历年高考的常见题型，解题关键是熟练应用等差数列的性质，灵活转化，裂项、分组数列求和的常用方法，把数列求和与不等式结合，也是近几年高考的趋势．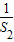