
定义在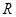 上奇函数
上奇函数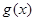 与偶函数
与偶函数 ,对任意
,对任意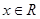 满足
满足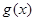 +
+
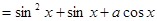 a为实数
a为实数
(1)求奇函数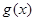 和偶函数
和偶函数 的表达式
的表达式
(2)若a>2, 求函数 在区间
在区间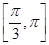 上的最值
上的最值
(1) =sin2x+acosx ,
=sin2x+acosx ,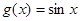 ;
;
(2)当cosx="-1" ,h(x)min=-a,当cosx=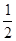 , h(x)max=
, h(x)max=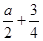 。
。
解析试题分析:(1)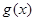 +
+
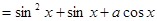 ①
①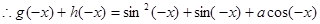
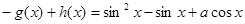 ② 3分
② 3分
联立①②得 =sin2x+acosx 5分
=sin2x+acosx 5分 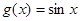 7分
7分
(2) =1-cos2x+acosx=-(cosx-
=1-cos2x+acosx=-(cosx-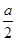 )2+
)2+ +1 9分
+1 9分
若a>1,则对称轴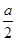 >1,且x
>1,且x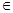
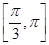 时,cosx
时,cosx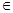 [-1,
[-1,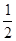 ] 11分
] 11分
当cosx="-1" ,h(x)min=-a,当cosx=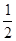 , h(x)max=
, h(x)max=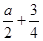 14分
14分
考点:本题主要考查函数的奇偶性,三角函数的图象和性质,二次函数的图象和性质。
点评:中档题,根据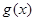 +
+ 求奇函数
求奇函数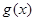 与偶函数
与偶函数 ,方法是列方程组。(2)利用换元思想,将问题转化成求二次函数在闭区间的最值问题。
,方法是列方程组。(2)利用换元思想,将问题转化成求二次函数在闭区间的最值问题。


科目:高中数学 来源: 题型:解答题
已知函数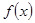 是定义在
是定义在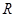 上的偶函数,且当
上的偶函数,且当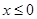 时,
时,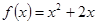 .现已画出函数
.现已画出函数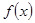 在
在 轴左侧的图像,如图所示,并根据图像
轴左侧的图像,如图所示,并根据图像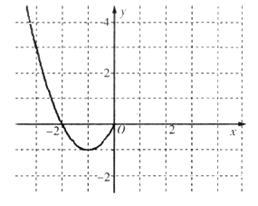
(1)写出函数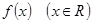 的增区间;
的增区间;
(2)写出函数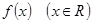 的解析式;
的解析式;
(3)若函数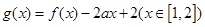 ,求函数
,求函数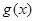 的最小值。
的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com