
(本小题共9分)
已知函数f(x)=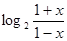 。
。
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)判断函数f(x)的奇偶性,并证明;
(Ⅲ)判断函数f(x)在定义域上的单调性,并用定义证明。
(1)x∈(-1,1)(2)奇函数(3)根据函数的定义法加以证明,一设二作差,三变形,四定号来完成,并下结论,属于基础题。
解析试题分析:解:(Ⅰ)由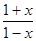 >0,解得-1<x<1,所以f(x)的定义域是(-1,1) 3分
>0,解得-1<x<1,所以f(x)的定义域是(-1,1) 3分
证明:(Ⅱ)由(Ⅰ)知x∈(-1,1)
又因为f(-x)= 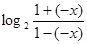 =
=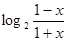 =
=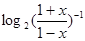 =-
=-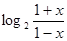 =-f(x).
=-f(x).
所以函数f(x)是奇函数。 6分
(Ⅲ)设-1<x<x<1,
f(x)-f(x)=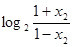 -
-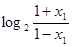 =
=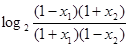
因为1-x>1-x>0;1+ x>1+ x>0,
所以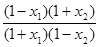 >1. 所以
>1. 所以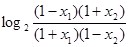 >0.
>0.
所以函数f(x)= 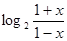 在(-1,1)上是增函数. 9分
在(-1,1)上是增函数. 9分
考点:函数概念和性质的运用
点评:解决该试题的关键是能利用函数的性质来分析证明函数单调性以及奇偶性的判定,属于基础题。


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
(本小题满分14分)
已知函数 ,其中e是自然数的底数,
,其中e是自然数的底数, .
.
(1)当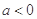 时,解不等式
时,解不等式 ;
;
(2)当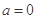 时,求正整数k的值,使方程
时,求正整数k的值,使方程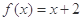 在[k,k+1]上有解;
在[k,k+1]上有解;
(3)若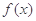 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com