
 (a>1)的左右焦点为F1,F2,抛物线C:y2=2px以F2为焦点.
(a>1)的左右焦点为F1,F2,抛物线C:y2=2px以F2为焦点.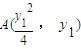 ,
,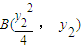 ,则
,则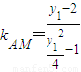 =
=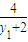 ,
,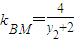 ,由△MPQ是以MP,MQ为腰的等腰三角形,可得kMA=-kMB,以下同上.
,由△MPQ是以MP,MQ为腰的等腰三角形,可得kMA=-kMB,以下同上.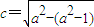 =1,
=1,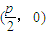 ,∴
,∴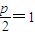 ,解得p=2,∴抛物线C的标准方程为:y2=4x.
,解得p=2,∴抛物线C的标准方程为:y2=4x.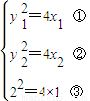
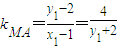 ④
④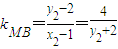 ⑤
⑤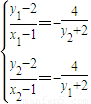 化简整理,
化简整理,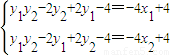
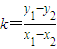 =
=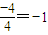 为定值.
为定值.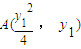 ,
,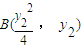 ,
,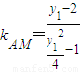 =
=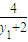 ,
,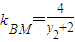 ,
,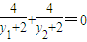
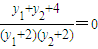
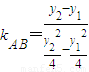 =
=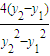 =
=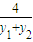 =
=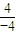 =-1.
=-1.

 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省漳州市立人学校高二(下)月考数学试卷(解析版) 题型:解答题
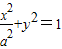 (a>0)的离心率为
(a>0)的离心率为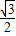 .
.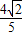 ,求直线l的倾斜角.
,求直线l的倾斜角.查看答案和解析>>
科目:高中数学 来源:2012年吉林省高考数学模拟试卷2(文科)(解析版) 题型:解答题
 (a>0)的离心率为
(a>0)的离心率为 .
. ,求直线l的倾斜角.
,求直线l的倾斜角.查看答案和解析>>
科目:高中数学 来源:2011年吉林省长春市高三第一次调研数学试卷(文科)(解析版) 题型:解答题
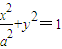 (a>0)的离心率为
(a>0)的离心率为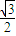 .
.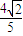 ,求直线l的倾斜角.
,求直线l的倾斜角.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com