已知Sn为数列{an}的前n项和,且Sn=2an+n2-3n-2(n∈N*)
(I)求证:数列{an-2n}为等比数列;
(II)设bn=an•cosnπ,求数列{bn}的前n项和Pn.
解:(I)∵S
n=2a
n+n
2-3n-2①∴S
n+1=2a
n+1+(n+1)
2-3(n+1)-2
两式相减,得a
n+1=2a
n+1-2a
n+2n-2,∴a
n+1=2a
n-2n+2
故a
n+1-2(n+1)=2(a
n-2n),又在①式中令n=1得a
1=4,∴a
1-2≠0∴
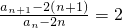
,
∴{a
n-2n}为等比数列
(II)由(I)知:a
n-2n=2•2
n-1,∴a
n=2
n+2n且cosnπ=(-1)
n当n为偶数时,设n=2k(k∈N
*)
则P
n=b
1+b
2+…+b
n=(b
1+b
3+…+b
2k-1)+(b
2+b
4+…+b
2k)={-(2+2×1)-(2
3+2×3)-…-[2
2k-1+2(2k-1)]}+[(2
2+2×2)+(2
4+2×4)+…+(2
2k+2k)]=-(2+2
3+…+2
2k-1)-2[1+3+…+(2k-1)]+(2
2+2
4+…+2
2k)+2(2+4+…+2k)=-(2-2
2+2
3-2
4+…+2
2k-1-2
2k)+2[-1+2-3+4-…-(2k-1)+2k]=
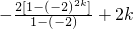
=
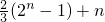
当n为奇数时,设n=2k-1(k∈N
*),同理可得
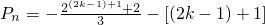
=
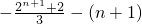
=
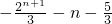
综上所述,
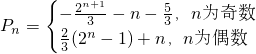
分析:(I)将S
n=2a
n+n
2-3n-2利用数列中a
n,Sn的关系进行转化构造出新数列{a
n-2n},再据其性质证明.
(Ⅱ)将(I)中所求的a
n代入bn,分组求和法求和.
点评:本题考查等比数列的判断、数列求和,转化,计算的能力.

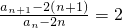 ,
,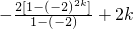 =
=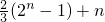
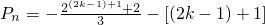 =
=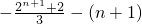 =
=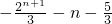
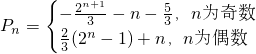


 名校通行证有效作业系列答案
名校通行证有效作业系列答案