
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的值;
的值;
(2)如果当![]() ,且
,且![]() 时,
时, ![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)根据导数的运算法则,求出函数![]() 的导数,利用切线方程求出切线的斜率及切点坐标,利用函数在切点处的导数值为曲线切线的斜率及切点也在曲线上,列出关于
的导数,利用切线方程求出切线的斜率及切点坐标,利用函数在切点处的导数值为曲线切线的斜率及切点也在曲线上,列出关于![]() 的方程组,即可求出
的方程组,即可求出![]() 值;(2) 由(1)知
值;(2) 由(1)知![]() ,所以
,所以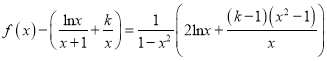 ,考虑函数
,考虑函数![]() ,则
,则![]() ,分三种情况
,分三种情况![]() ,
, ![]() ,
, ![]() ,分别利用导数研究函数的单调性,根据单调性求出函数
,分别利用导数研究函数的单调性,根据单调性求出函数![]() 的最小值,排除不合题意的
的最小值,排除不合题意的![]() 的范围,筛选出符合题意的
的范围,筛选出符合题意的![]() 的范围即可.
的范围即可.
试题解析:(1)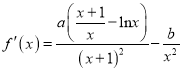 ,
,
由于直线![]() 的斜率为
的斜率为![]() ,且过点
,且过点![]() ,
,
故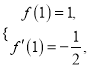 即
即
解得![]() .
.
(2)由(1)知![]() ,所以
,所以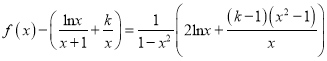 .
.
考虑函数![]() ,则
,则![]() .
.
(ⅰ)设![]() ,由
,由![]() 知,当
知,当![]() 时,
时, ![]() .而
.而![]() ,故
,故
当![]() 时,
时, ![]() ,可得
,可得![]() ;
;
当![]() 时,
时, ![]() ,可得
,可得![]()
从而当![]() ,且
,且![]() 时,
时, ![]() ,即
,即![]() .
.
(ⅱ)设![]() .由于当
.由于当![]() 时,
时, ![]() ,故
,故![]() ,而
,而![]() ,
,
故当![]() 时,
时, ![]() ,可得
,可得![]() ,与题设矛盾.
,与题设矛盾.
(ⅲ)设![]() .此时
.此时![]() ,而
,而![]() ,故当
,故当![]() 时,
时, ![]() ,可得
,可得![]() ,与题设矛盾.综合得,
,与题设矛盾.综合得, ![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】炼钢是一个氧化降碳的过程,钢水含碳量的多少直接影响冶炼时间的长短,必须掌握钢水含碳量和冶炼时间的关系.如果已测得炉料溶化完毕时钢水的含碳量x与冶炼时间y(从炉料溶化完毕到出钢的时间)的一组数据,如表所示:
x(0.01%) | 104 | 180 | 190 | 177 | 147 | 134 | 150 | 191 | 204 | 121 |
y/min | 100 | 200 | 210 | 185 | 155 | 135 | 170 | 205 | 235 | 125 |
(1)y与x是否具有线性相关关系?
(2)如果y与x具有线性相关关系,求回归直线方程.
(3)预报当钢水含碳量为160个0.01%时,应冶炼多少分钟?
参考公式:r=![]()
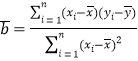 ,
,
线性回归方程![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点![]() ,
, ![]() ,
, ![]() 分别是椭圆的左、右焦点,以原点为圆心,椭圆
分别是椭圆的左、右焦点,以原点为圆心,椭圆![]() 的短轴长为直径的圆与直线
的短轴长为直径的圆与直线![]() 相切.
相切.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() ,求
,求![]() 内切圆面积的最大值和此时直线
内切圆面积的最大值和此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,且Sn=4an﹣p,其中p是不为零的常数.
(1)证明:数列{an}是等比数列;
(2)当p=3时,若数列{bn}满足bn+1=bn+an(n∈N*),b1=2,求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)求曲线![]() 在点
在点![]() 处的切线的斜率;
处的切线的斜率;
(Ⅱ)判断方程![]() (
(![]() 为
为![]() 的导数)在区间
的导数)在区间![]() 内的根的个数,说明理由;
内的根的个数,说明理由;
(Ⅲ)若函数![]() 在区间
在区间![]() 内有且只有一个极值点,求
内有且只有一个极值点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com