Question

【题目】如图，已知正三棱锥P﹣ABC的侧面是直角三角形，PA=6，顶点P在平面ABC内的正投影为点D，D在平面PAB内的正投影为点E，连接PE并延长交AB于点G．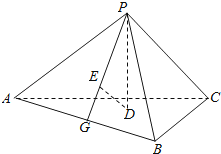

（1）证明：G是AB的中点；
（2）在图中作出点E在平面PAC内的正投影F（说明作法及理由），并求四面体PDEF的体积．

Answer 1

【答案】
（1）

证明：∵P﹣ABC为正三棱锥，且D为顶点P在平面ABC内的正投影，

∴PD⊥平面ABC，则PD⊥AB，

又E为D在平面PAB内的正投影，

∴DE⊥面PAB，则DE⊥AB，

∵PD∩DE=D，

∴AB⊥平面PDE，连接PE并延长交AB于点G，

则AB⊥PG，

又PA=PB，

∴G是AB的中点；

（2）

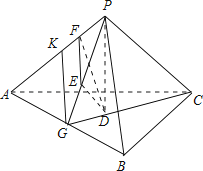∵正三棱锥P﹣ABC的侧面是直角三角形，

∴PB⊥PA，PB⊥PC，则PB⊥平面PAC，

而PB平面PAB，则平面PAB⊥平面PAC，

在平面PAB中，过E作EF⊥PA，则EF⊥平面PAC，

即F为E在平面PAC内的正投影．

由于PA=PB=PC=6，故AB=BC=AC=6 ，

易知PG= =3 ，GD= = ，由勾股定理得PD= =2 ，

【解析】（Ⅰ）根据题意分析可得PD⊥平面ABC，进而可得PD⊥AB，同理可得DE⊥AB，结合两者分析可得AB⊥平面PDE，进而分析可得AB⊥PG，又由PA=PB，由等腰三角形的性质可得证明；（2）由线面垂直的判定方法可得PB⊥平面PAC，进而由于PB平面PAB，可得平面PAB⊥平面PAC，由此可以在平面PAB中，过E作EF⊥PA，可得F为E在平面PAC内的正投影．
进而由棱锥的体积公式计算可得答案．；本题考查几何体的体积计算以及线面垂直的性质、应用，解题的关键是正确分析几何体的各种位置、距离关系．