
【题目】已知函数![]() .
.
(Ⅰ)若![]() 为函数
为函数![]() 的极值点,求
的极值点,求![]() 的值;
的值;
(Ⅱ)讨论![]() 在定义域上的单调性.
在定义域上的单调性.
【答案】(Ⅰ) ![]() ;(Ⅱ) ①当
;(Ⅱ) ①当![]() 时,
时, ![]() ,
, ![]() 递增;若
递增;若![]() ,
, ![]() 递减;②当
递减;②当![]() 时,若
时,若![]() ,
, ![]() 递减;若
递减;若![]() ,
, ![]() 递增;若
递增;若![]() ,
, ![]() 递减;③当
递减;③当![]() 时,
时, ![]() 在
在![]() 内递减;④当
内递减;④当![]() 时,
时, ![]() ,
, ![]() 递减;若
递减;若![]() ,
, ![]() 递增;
递增;
若![]() ,
, ![]() 递减.
递减.
【解析】试题分析:
(1)由题意可得![]() ,解得
,解得![]() .注意检验a的正确性.
.注意检验a的正确性.
(2)导函数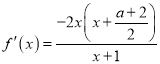 ,分类讨论可得:
,分类讨论可得:
①当![]() 时,
时, ![]() ,
, ![]() 递增;若
递增;若![]() ,
, ![]() 递减;
递减;
②当![]() 时,若
时,若![]() ,
, ![]() 递减;若
递减;若![]() ,
, ![]() 递增;若
递增;若![]() ,
, ![]() 递减;
递减;
③当![]() 时,
时, ![]() 在
在![]() 内递减;
内递减;
④当![]() 时,
时, ![]() ,
, ![]() 递减;若
递减;若![]() ,
, ![]() 递增;若
递增;若![]() ,
, ![]() 递减.
递减.
试题解析:
(Ⅰ)因为![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() .
.
经检验:当![]() 时,
时, ![]() 递增;
递增;
当![]() 时,
时, ![]() 递减.
递减.
所以![]() 在
在![]() 处取最大值.
处取最大值.
所以![]() 满足题意.
满足题意.
(Ⅱ) 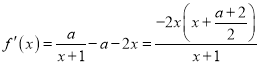 ,
,
令![]() ,得
,得![]() 或
或![]() ,
,
又![]() 的定义域为
的定义域为![]() .
.
①当![]() ,即
,即![]() 时,
时,
若![]() ,则
,则![]() 递增;
递增;
若![]() ,则
,则![]() 递减;
递减;
②当![]() ,即
,即![]() 时,
时,
若![]() ,则
,则![]() 递减;
递减;
若![]() ,则
,则![]() 递增;
递增;
若![]() ,则
,则![]() 递减;
递减;
③当![]() ,即
,即![]() 时,
时,
![]() ,
, ![]() 在
在![]() 内递减;
内递减;
④当![]() ,即
,即![]() 时,
时,
若![]() ,则
,则![]() 递减;
递减;
若![]() ,则
,则![]() 递增;
递增;
若![]() ,则
,则![]() 递减.
递减.


科目:高中数学 来源: 题型:
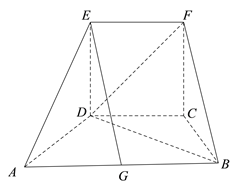
【题目】如图所示的几何体中,四边形![]() 为等腰梯形,
为等腰梯形, ![]() ∥
∥![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() .
.
(Ⅰ)若点![]() 是棱
是棱![]() 的中点,求证:
的中点,求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在国家“大众创业,万众创新”战略下,某企业决定加大对某种产品的研发投入,已知研发投入![]() (十万元)与利润
(十万元)与利润![]() (百万元)之间有如下对应数据:
(百万元)之间有如下对应数据:
| 2 | 3 | 4 | 5 | 6 |
| 2 | 4 | 5 | 6 | 7 |
若由资料知![]() 对
对![]() 呈线性相关关系。试求:
呈线性相关关系。试求:
(1)线性回归方程![]() ;
;
(2)估计![]() 时,利润是多少?
时,利润是多少?
附:利用“最小二乘法”计算a,b的值时,可根据以下公式:
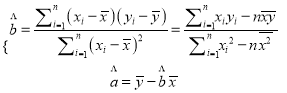
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)判断函数f(x)在区间[1,+∞)上的单调性,并用定义证明你的结论;
(2)求函数f(x)在区间[2,4]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月产量如表(单位:辆):
轿车A | 轿车B | 轿车C | |
舒适型 | 100 | 150 | z |
标准型 | 300 | 450 | 600 |
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆。
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本。将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设偶函数f(x)满足f(x)=x3﹣8(x≥0),则{x|f(x﹣2)>0}=( )
A.{x|x<﹣2或x>4}
B.{x|x<0或x>4}
C.{x|x<0或x>6}
D.{x|x<﹣2或x>2}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2﹣ax+3,且对任意的实数x都有f(4﹣x)=f(x)成立.
(1)求实数a的值;
(2)求函数f(x)在区间[0,3]上的值域;
(3)要得到函数y=x2的图象只需要将二次函数y=f(x)的图象做怎样的变换得到.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com