
【题目】已知函数![]() ,
,![]() .
.
(1)解不等式:![]()
(2)是否存在实数t,使得不等式![]()
![]() ,对任意的
,对任意的![]() 及任意锐角
及任意锐角![]() 都成立,若存在,求出t的取值范围:若不存在,请说明理由.
都成立,若存在,求出t的取值范围:若不存在,请说明理由.
【答案】(1)![]() (2)存在,
(2)存在,![]()
【解析】
(1)根据题意,先求出![]() 的解析式,并判断
的解析式,并判断![]() 的奇偶性和单调性,结合奇偶性和单调性,即可求解;
的奇偶性和单调性,结合奇偶性和单调性,即可求解;
(2)法一:通过反证法,先假设存在正实数t,使得该不等式对任意的![]() 及任意锐角
及任意锐角![]() 都成立,化简原不等式,通过推理论证,与
都成立,化简原不等式,通过推理论证,与![]() 和对任意的
和对任意的![]() 及任意锐角
及任意锐角![]() ,是否矛盾,得出存在
,是否矛盾,得出存在![]() ,且可求出
,且可求出![]() 的取值范围.
的取值范围.
法二:先化简原不等式,通过换元,构造新二次函数![]() ,通过新函数
,通过新函数![]() 恒成立,转化成二次函数恒成立问题,即可得出存在
恒成立,转化成二次函数恒成立问题,即可得出存在![]() ,且可求出
,且可求出![]() 的取值范围.
的取值范围.
(1)![]() ,
,![]() 为
为![]() 上的奇函数
上的奇函数
又![]() 为R上的增函数
为R上的增函数
于是![]()
![]()
![]()
![]()
故原不等式的解集为![]()
(2)假设存在正实数t,使得该不等式对任意的![]() 及任意锐角
及任意锐角![]() 都成立
都成立
原不等式![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 不等式不可能成立,故
不等式不可能成立,故![]()
![]()
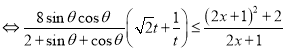
![]()
![]() 不等式对任意的
不等式对任意的![]() 都成立
都成立
![]()
故![]()
而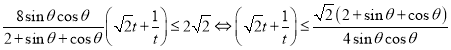
该不等式对任意锐角![]() 都成立
都成立
所以
令![]() ,则
,则
![]()
设![]() ,令
,令![]() ,
,![]()
则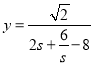 ,而
,而![]() 在
在![]() 单调递增
单调递增
故![]()
所以![]() ,即
,即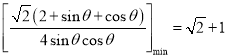
故![]() ,又
,又![]()
![]()
法二:原不等式![]()
![]()
![]()
令![]() ,
,![]()
原不等式
![]()
![]() 时,
时,![]() 不成立,
不成立,![]() 也不可能成立
也不可能成立
故![]()
令![]()
即![]() 恒成立
恒成立
若方程![]() 的
的![]() ,但其两根和与两根积都大于0,开口向上
,但其两根和与两根积都大于0,开口向上
故![]() 不可能在
不可能在![]() 上恒成立
上恒成立
所以![]() 在
在![]() 上恒成立
上恒成立
![]() 对任意锐角
对任意锐角![]() 恒成立
恒成立
![]()
![]()
同法一可得:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知倾斜角为![]() 的直线
的直线![]() 过点
过点![]() 和点
和点![]() ,点
,点![]() 在第一象限,
在第一象限,![]() .
.
(1)求![]() 的坐标;
的坐标;
(2)若直线![]() 与两平行直线
与两平行直线![]() ,
,![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值;
的值;
(3)记集合![]() 直线
直线![]() 经过点
经过点![]() 且与坐标轴围成的面积为
且与坐标轴围成的面积为![]() ,
,![]() ,针对
,针对![]() 的不同取值,讨论集合
的不同取值,讨论集合![]() 中的元素个数.
中的元素个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是水资源匮乏国家,节约用水是每个中国公民应有的意识.为了保护水资源,提倡节约用水,某城市对居民生活用水实行“阶梯水价”,计费方法如下表:
每户每月用水量 | 水价 |
不超过12 | 3元/ |
超过12 | 6元/ |
超过18 | 9元/ |
(1)该城市居民小张家月用水量记为![]() ,应交纳水费y(元),试建立y与x的函数解析式,并作出其图像;
,应交纳水费y(元),试建立y与x的函数解析式,并作出其图像;
(2)若小张家十月份交纳水费90元,求他家十月份的用水量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上恰有一个实数解,求
上恰有一个实数解,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若存在
,若存在![]() 使得函数
使得函数![]() 在区间
在区间![]() 上的最大值和最小值的差不超过1,求
上的最大值和最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点M(0,2),N(-2,0),直线l:kx-y-2k+2=0(k为常数).
(1)若点M,N到直线l的距离相等,求实数k的值;
(2)对于l上任意一点P,∠MPN恒为锐角,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com