
在△ABC中,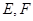 分别是
分别是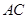 ,
,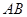 的中点,且
的中点,且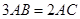 ,若
,若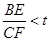 恒成立,则
恒成立,则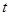 的最小值为( )
的最小值为( )
A. 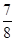 B.
B.
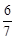 C.
C.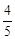 D.
D.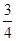
A
【解析】
试题分析:如图所示:
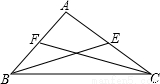
∵3AB=2AC,∴AC= 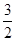 AB,
AB,
又E、F分别为AC、AB的中点,
∴AE= 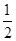 AC,AF=
AC,AF=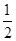 AB,
AB,
∴在△ABE中,由余弦定理得:BE2=AB2+AE2-2AB•AE•cosA
=AB2+(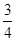 AB)2-2AB•
AB)2-2AB• 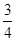 AB•cosA=
AB•cosA=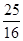 AB2-
AB2-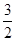 AB2cosA,
AB2cosA,
在△ACF中,由余弦定理得:CF2=AF2+AC2-2AF•AC•cosA
=(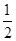 AB)2+(
AB)2+(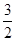 AB)2-2•
AB)2-2•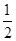 AB•
AB•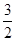 AB•cosA=
AB•cosA=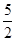 AB2-
AB2-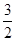 AB2cosA,
AB2cosA,
∴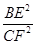 =
=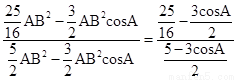 ,
,
∴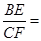
 =
=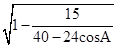 .
.
∵当cosA取最小值时,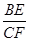 最大,
最大,
∴当A→π时,cosA→-1,此时 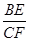 达到最大值,最大值为
达到最大值,最大值为 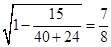 ,
,
故 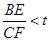 恒成立,t的最小值为
恒成立,t的最小值为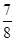 .选A.
.选A.
考点:余弦定理,余弦函数的性质,不等式恒成立问题。
点评:中档题,不等式恒成立问题,往往通过“分离参数”,转化成求函数的最值问题,解答本题的关键是,熟练掌握余弦定理,利用余弦定理建立三角形的边角关系。


科目:高中数学 来源: 题型:
(09年山东苍山期末文)(12分)
设函数![]() 其中向量
其中向量![]() ,
,![]() ,
,![]() 。
。
(1)求![]() 的最小正周期与单调减区间;
的最小正周期与单调减区间;
(2)在△ABC中,![]() 分别是角A、B、C的对边,已知
分别是角A、B、C的对边,已知![]() ,
,![]() ,△ABC的面积是为
,△ABC的面积是为![]() ,求
,求![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三第四次(12月)阶段性测试数学试卷(解析版) 题型:解答题
在△ABC中,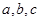 分别是角A,B,C的对边,
分别是角A,B,C的对边,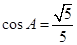 ,
,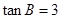 .
.
(Ⅰ)求角 的值;
的值;
(Ⅱ)若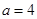 ,求△ABC面积.
,求△ABC面积.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川宜宾高三第二次模拟考试理科数学试卷(解析版) 题型:解答题
已知函数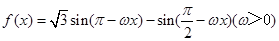 的图像上两相邻最高点的坐标分别为
的图像上两相邻最高点的坐标分别为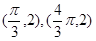 .
.
(Ⅰ)求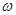 的值;
的值;
(Ⅱ)在△ABC中,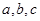 分别是角A,B,C的对边,且
分别是角A,B,C的对边,且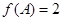 求
求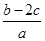 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012届安徽省高三第一学期期中文科数学试卷 题型:解答题
已知函数
(I)求 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(II)在△ABC中, 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若 △ABC的面积为
△ABC的面积为 ,求
,求 的值
的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com