
(12分)正方形ABCD边长为4,点E是边CD上的一点,
将![]() AED沿AE折起到
AED沿AE折起到![]() 的位
的位![]() 置时,有平面
置时,有平面![]()
![]() 平面ABCE,
平面ABCE,
并且![]()
![]()
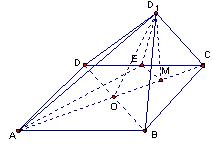
![]() (如图)
(如图)
(I)判断并证明E点的具体位置;(II)![]() 求点D/到平面ABCE的距离.
求点D/到平面ABCE的距离.
(I)略 (II)![]()
(I)连结AC、BD交于点O,再连DD![]() ,由BD
,由BD![]() AC,且平面ACD
AC,且平面ACD![]()
![]() 平面ABCE于AC,∴BD
平面ABCE于AC,∴BD![]() 平面ACD
平面ACD![]() ,故C
,故C![]() D
D![]()
![]() BD,又CD
BD,又CD![]()
![]() BD
BD![]() ,∴CD
,∴CD![]()
![]() 平面BDD
平面BDD![]() ,[来源:学即得CD
,[来源:学即得CD![]()
![]() DD
DD![]() ,在Rt△CDD
,在Rt△CDD![]() 中,由于ED=ED
中,由于ED=ED![]() ,∴∠EDD
,∴∠EDD![]() =∠ED
=∠ED![]() D,
D,
则∠ECD![]() =900
=900![]() EDD
EDD![]() =900
=900![]() ED
ED![]() D=∠ED
D=∠ED![]() C,∴EC=ED
C,∴EC=ED![]() =ED,
=ED,
即E点为边CD的中点. …………………6分
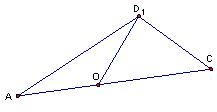
 (II)方法一:如图取OC的中
(II)方法一:如图取OC的中![]() 点M,连结D
点M,连结D![]() M、EM,
M、EM,
则EM//BD,得EM![]() 平面ACD
平面ACD![]() ,
,
即∠EMD![]() =900,又因为D
=900,又因为D![]() E=2,EM
E=2,EM![]() =
=![]() ,
,
则D![]() M=
M=![]() ,又AD
,又AD![]()
![]() EM,∵AD
EM,∵AD![]() DE,
DE,
∴ AD![]()
![]() D
D![]() E,∴AD
E,∴AD![]()
![]() 平
平![]() 面EMD
面EMD![]() ,
,
则AD![]()
![]() D
D![]() M,在Rt△AMD
M,在Rt△AMD![]() 中,AD
中,AD![]() =4,AM=
=4,AM=![]() ,D
,D![]() M=
M=![]() ,
,
过D![]() 作D
作D![]() H
H![]() AM于H点,则D
AM于H点,则D![]() H
H![]() 平面ABCE,
平面ABCE,
由于D![]() H=
H=![]() ,此即得点D
,此即得点D![]() 到平面ABCE的距离.
到平面ABCE的距离.
 方法二:如图, 连结OD
方法二:如图, 连结OD![]() ,∵CD
,∵CD![]()
![]() 平面BDD
平面BDD![]() ,
,
∴CD![]()
![]() OD
OD![]() ,
,
在△AD![]() C中,设OD
C中,设OD![]()
![]() ,
,
则∵OC![]() ,∴CD
,∴CD![]() =
=![]() ,
,
∵∠AOD![]() 与∠D
与∠D![]() OC互补,
OC互补,
由余弦定理得![]() ,
,
解得![]() ,在直角三角形OD
,在直角三角形OD![]() C中,
C中,
由![]() 面积公式得所求距离为
面积公式得所求距离为![]() .
.
 方法三:能用最小角定理
方法三:能用最小角定理![]() 帮助解△AD
帮助解△AD![]() C,
C,
即![]() ,其中
,其中![]()
可求.
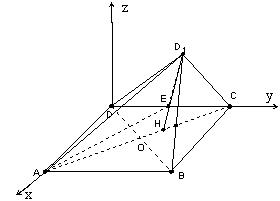
另解: 建立如图所示的空间直角坐标系,则D(0,0,0),
A(4,0,0),B(4,4,0),C(0,4,0),
设E(0,![]() ,0),D
,0),D![]() (
(![]() ),
),
设D![]() H
H![]() 平面ABCE于H点,则H在AC上,
平面ABCE于H点,则H在AC上,
∴H的坐标为(![]() ,0),依题意有:
,0),依题意有:
![]() ,
,![]() ,
,![]() ,
,![]() ,[来源:Zxxk.Com]
,[来源:Zxxk.Com]
∵![]()
![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,[来源:学科网]
,[来源:学科网]
![]() ,∴
,∴![]() ,
,
![]() ,∴
,∴![]()
由![]() 与
与![]() 两式相减,
两式相减,
将![]() 代入得
代入得![]() ,从而有
,从而有![]() ,
,
即E为CD![]() 中点,点D
中点,点D![]() 到平面ABCE的距离是
到平面ABCE的距离是![]() . …………………12分
. …………………12分


科目:高中数学 来源: 题型:
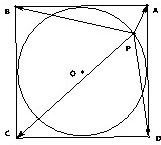 如图,正方形ABCD边长为2,内切圆为⊙O,点P是⊙O上任意一点.
如图,正方形ABCD边长为2,内切圆为⊙O,点P是⊙O上任意一点.| PA |
| PB |
| PC |
| PD |
| PA |
| PB |
| PC |
| PD |
查看答案和解析>>
科目:高中数学 来源: 题型:
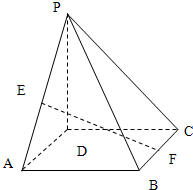 已知四棱锥P-ABCD中,PD⊥平面ABCD,正方形ABCD边长为2,PD=2,E,F分别是PA、BC的中点
已知四棱锥P-ABCD中,PD⊥平面ABCD,正方形ABCD边长为2,PD=2,E,F分别是PA、BC的中点查看答案和解析>>
科目:高中数学 来源: 题型:
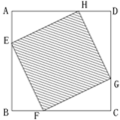 如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )
如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )查看答案和解析>>
科目:高中数学 来源: 题型:
| A、将△ABD沿BD翻转到任意位置时,直线AC与直线BD都垂直 | ||||
| B、当平面ABD垂直于平面BCD时,此时∠ACD=60° | ||||
C、沿BD翻转到某个位置时,使得三棱锥A-BCD体积最大值是
| ||||
| D、沿BD翻转到任意位置时,三直线“AB与CD”,“AD与BC”,“AC与BD”均不垂直 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com