
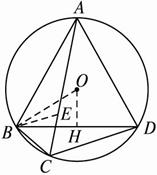
图2-2-5
(1)当⊙O的半径为8 cm时,求△ABD的内切圆面积;
(2)求证:AC =BC + CD.
思路解析:(1)要求内切圆面积,则先求内切圆半径和圆心,因此先研究△ABD的性质.(2)证明线段的和的问题,先在AC上截取CE =BC,然后再证AE =CD.
(1)解:过O点作OH⊥BD,垂足为H,连结BO.?
∵四边形ABCD为⊙O内接四边形,?
∴∠BAD +∠BCD =180°.?
∴∠BAD =60°.?
∵AB=AD,∴△ABD为正三角形.?
∴OH为△ABD的内切圆半径.?
在Rt△OBH中,OB =8 cm,∠OBH=30°,?
∴OH =4 cm.∴△ABD的内切圆面积为16πcm2.
(2)证明:在AC上截取CE =BC,连结BE.?
∵∠BCA =∠BDA =60°,∴△BCE为等边三角形.?
∴BE =BC.?
又∠BEA =∠BCD,∠BAE =∠BDC,?
∴△ABE≌△DBC.∴AE=CD.?
∴AC =AE +CE =CD +BC.


科目:高中数学 来源: 题型:

(1)四边形MNPQ是平行四边形吗?
(2)若AC=BD,能截得菱形吗?如果能,那么如何截?
(3)在什么情况下,可以截得一个矩形?
(4)在什么条件下,能截得一个正方形?如果能,该怎样截?(注:只需给出满足条件的一种情形即可)
(5)若AC=BD=a,求证:四边形MNPQ的周长为定值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省马鞍山市高一(上)期末数学试卷(解析版) 题型:选择题
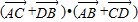 =( )
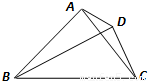
=( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com