
ΓΨΧβΡΩΓΩΈΣΝΥΚκ―οΟώΉεΈΡΜ·Θ§Ρ≥÷–―ßΨΌ––ΝΥΓΑΈ“Α°Ιζ―ßΘ§¥ΪΥ–Ψ≠ΒδΓ±ΩΦ ‘Θ§≤Δ¥”÷–ΥφΜζ≥ι»ΓΝΥ60Οϊ―ß…ζΒΡ≥…Φ®Θ®¬ζΖ÷100Ζ÷Θ©ΉςΈΣ―υ±ΨΘ§Τδ÷–≥…Φ®≤ΜΒΆ”Ύ80Ζ÷ΒΡ―ß…ζ±ΜΤάΈΣ”≈–ψ…ζΘ§ΒΟΒΫ≥…Φ®Ζ÷≤ΦΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ»γΆΦΥυ ΨΘ°

Θ®1Θ©»τΗΟΥυ÷–―ßΙ≤”–2000Οϊ―ß…ζΘ§ ‘άϊ”Ο―υ±ΨΙάΦΤ»Ϊ–Θ’β¥ΈΩΦ ‘÷–”≈–ψ…ζ»Υ ΐΘΜ
Θ®2Θ©Θ®iΘ© ‘ΙάΦΤ’β¥Έ≤ΈΦ”ΩΦ ‘ΒΡ―ß…ζΒΡΤΫΨυ≥…Φ®Θ®Ά§“ΜΉι ΐΨί”ΟΗΟΉι«χΦδΒΡ÷–Βψ÷ΒΉς¥ζ±μΘ©ΘΜ
Θ®iiΘ©»τ‘Ύ―υ±Ψ÷–Θ§άϊ”ΟΖ÷≤ψ≥ι―υΒΡΖΫΖ®¥”≥…Φ®≤ΜΒΆ”Ύ70Ζ÷ΒΡ―ß…ζ÷–ΥφΜζ≥ι»Γ6»ΥΘ§‘Ό¥”÷–≥ι»Γ3»Υ‘υΥΆ“ΜΧΉΙζ―ßΨ≠Βδ―ßΦ°Θ§ ‘«σ«ΓΚΟ≥ι÷–2Οϊ”≈–ψ…ζΒΡΗ≈¬ Θ°
ΓΨ¥πΑΗΓΩ(1)600ΘΜ(2)(i)72.5ΘΜ(ii)![]() .
.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©”…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§ΤΒ¬ =Θ®ΤΒ ΐΘ©/(―υ±Ψ»ίΝΩ)Θ§Ά®Ιΐ![]() ΒΡΤΒ¬ Θ§Ω…«σΒΟ”≈–ψ»Υ ΐΓΘΘ®2Θ©”…ΤΫΨυ ΐΙΪ Ϋ«σΒΟΤΫΨυ≥…Φ®Θ§Θ©”…Ζ÷≤ψ≥ι―υ≥ιΤπ≥…Φ®‘Ύ
ΒΡΤΒ¬ Θ§Ω…«σΒΟ”≈–ψ»Υ ΐΓΘΘ®2Θ©”…ΤΫΨυ ΐΙΪ Ϋ«σΒΟΤΫΨυ≥…Φ®Θ§Θ©”…Ζ÷≤ψ≥ι―υ≥ιΤπ≥…Φ®‘Ύ![]() Θ§
Θ§![]() Θ§
Θ§![]() ΦδΖ÷±π≥ι»ΓΝΥ3»ΥΘ§2»ΥΘ§1»ΥΘ°‘Ό”…ΟΕΨΌΖ®Ν–ΨΌ≥ω6―Γ3ΒΡΥυ”–«ιΩωΘ§ΉνΚσ”ΟΙ≈ΒδΗ≈–ΆΙΪ Ϋ«σΒΟΗ≈¬ ΓΘ
ΦδΖ÷±π≥ι»ΓΝΥ3»ΥΘ§2»ΥΘ§1»ΥΘ°‘Ό”…ΟΕΨΌΖ®Ν–ΨΌ≥ω6―Γ3ΒΡΥυ”–«ιΩωΘ§ΉνΚσ”ΟΙ≈ΒδΗ≈–ΆΙΪ Ϋ«σΒΟΗ≈¬ ΓΘ
‘ΧβΫβΈω;Θ®1Θ©”…÷±ΖΫΆΦΩ…÷ΣΘ§―υ±Ψ÷– ΐΨί¬δ‘Ύ![]() ΒΡΤΒ¬ ΈΣ
ΒΡΤΒ¬ ΈΣ![]() Θ§
Θ§
‘ρΙάΦΤ»Ϊ–Θ’β¥ΈΩΦ ‘÷–”≈–ψ…ζ»Υ ΐΈΣ![]() Θ°
Θ°
Θ®2Θ©Θ®iΘ©…η―υ±Ψ ΐΨίΒΡΤΫΨυ ΐΈΣ![]() Θ§
Θ§
‘ρ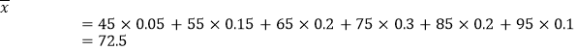 Θ§
Θ§
‘ρΙάΦΤΥυ”–≤ΈΦ”ΩΦ ‘ΒΡ―ß…ζΒΡΤΫΨυ≥…Φ®ΈΣ72.5Θ°
Θ®iiΘ©”…Ζ÷≤ψ≥ι―υ÷Σ ΕΩ…÷ΣΘ§≥…Φ®‘Ύ![]() Θ§
Θ§![]() Θ§
Θ§![]() ΦδΖ÷±π≥ι»ΓΝΥ3»ΥΘ§2»ΥΘ§1»ΥΘ°
ΦδΖ÷±π≥ι»ΓΝΥ3»ΥΘ§2»ΥΘ§1»ΥΘ°
Φ«≥…Φ®‘Ύ![]() ΒΡ3»ΥΈΣ
ΒΡ3»ΥΈΣ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§≥…Φ®‘Ύ
Θ§≥…Φ®‘Ύ![]() ΒΡ2»ΥΈΣ
ΒΡ2»ΥΈΣ![]() Θ§
Θ§![]() Θ§≥…Φ®‘Ύ
Θ§≥…Φ®‘Ύ![]() ΒΡ1»ΥΈΣ
ΒΡ1»ΥΈΣ![]() Θ§
Θ§
‘ρ¥”’β6»Υ÷–≥ι»Γ3»ΥΒΡΥυ”–Ω…ΡήΫαΙϊ”–![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Ι≤20÷÷Θ§
Ι≤20÷÷Θ§
Τδ÷–«ΓΚΟ≥ι÷–2Οϊ”≈–ψ…ζΒΡΫαΙϊ”–![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Ι≤9÷÷Θ§
Ι≤9÷÷Θ§
Υυ“‘«ΓΚΟ≥ι÷–2Οϊ”≈–ψ…ζΒΡΗ≈¬ ΈΣ![]() Θ°
Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τΆ÷‘≤![]() ΘΚ
ΘΚ![]() …œ”–“ΜΕ·Βψ
…œ”–“ΜΕ·Βψ![]() Θ§
Θ§![]() ΒΫΆ÷‘≤
ΒΫΆ÷‘≤![]() ΒΡΝΫΫΙΒψ
ΒΡΝΫΫΙΒψ![]() Θ§
Θ§![]() ΒΡΨύάκ÷°ΚΆΒ»”Ύ
ΒΡΨύάκ÷°ΚΆΒ»”Ύ![]() Θ§
Θ§![]() ΒΫ÷±œΏ
ΒΫ÷±œΏ![]() ΒΡΉν¥σΨύάκΈΣ
ΒΡΉν¥σΨύάκΈΣ![]() .
.
Θ®ΔώΘ©«σΆ÷‘≤ΒΡΖΫ≥ΧΘΜ
Θ®ΔρΘ©»τΙΐΒψ![]() ΒΡ÷±œΏ
ΒΡ÷±œΏ![]() ”κΆ÷‘≤
”κΆ÷‘≤![]() ΫΜ”Ύ≤ΜΆ§ΝΫΒψ
ΫΜ”Ύ≤ΜΆ§ΝΫΒψ![]() ΓΔ
ΓΔ![]() Θ§
Θ§![]() Θ®
Θ®![]() ΈΣΉχ±ξ‘≠ΒψΘ©«“
ΈΣΉχ±ξ‘≠ΒψΘ©«“![]() Θ§«σ Β ΐ
Θ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηa1 Θ§ a2 Θ§ Γ≠Θ§anΈΣ1Θ§2Θ§Γ≠Θ§nΑ¥»Έ“βΥ≥–ρΉω≥…ΒΡ“ΜΗω≈≈Ν–Θ§fk «Φ·Κœ{ai|aiΘΦak Θ§ iΘΨk}‘ΣΥΊΒΡΗω ΐΘ§Εχgk «Φ·Κœ{ai|aiΘΨak Θ§ iΘΦk}‘ΣΥΊΒΡΗω ΐΘ®k=1Θ§2Θ§Γ≠Θ§nΘ©Θ§ΙφΕ®fn=g1=0Θ§άΐ»γΘΚΕ‘”Ύ≈≈Ν–3Θ§1Θ§2Θ§f1=2Θ§f2=0Θ§f3=0
Θ®IΘ©Ε‘”Ύ≈≈Ν–4Θ§2Θ§5Θ§1Θ§3Θ§«σ![]()
![]()
Θ®IIΘ©Ε‘”Ύœν ΐΈΣ2n©¹1 ΒΡ“ΜΗω≈≈Ν–Θ§»τ“Σ«σ2n©¹1ΈΣΗΟ≈≈Ν–ΒΡ÷–ΦδœνΘ§ ‘«σ![]()
![]() ΒΡΉν¥σ÷ΒΘ§≤Δ–¥≥ωœύ”ΠΒΟ“ΜΗω≈≈Ν–
ΒΡΉν¥σ÷ΒΘ§≤Δ–¥≥ωœύ”ΠΒΟ“ΜΗω≈≈Ν–
Θ®ΔσΘ©÷ΛΟς![]()
![]() =
=![]()
![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…η![]() .
.
Θ®1Θ©«σ![]() ΒΡΒΞΒς«χΦδΘΜ
ΒΡΒΞΒς«χΦδΘΜ
Θ®2Θ©«σ![]() ‘Ύ[-5Θ§
‘Ύ[-5Θ§ ![]() ]ΒΡΉν¥σ÷Β”κΉν–Γ÷Β.
]ΒΡΉν¥σ÷Β”κΉν–Γ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ―Γ–ό4-4ΘΚΉχ±ξœΒ”κ≤Έ ΐΖΫ≥Χ
‘Ύ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§«ζœΏ
÷–Θ§«ζœΏ![]() ΒΡ≤Έ ΐΖΫ≥ΧΈΣ
ΒΡ≤Έ ΐΖΫ≥ΧΈΣ![]() Θ®
Θ®![]() ΈΣ≤Έ ΐΘ§
ΈΣ≤Έ ΐΘ§![]() Θ©Θ§“‘÷±Ϋ«Ήχ±ξœΒΒΡ‘≠ΒψΈΣΦΪΒψΘ§“‘
Θ©Θ§“‘÷±Ϋ«Ήχ±ξœΒΒΡ‘≠ΒψΈΣΦΪΒψΘ§“‘![]() ÷αΒΡ’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΉχ±ξœΒΘ§‘≤
÷αΒΡ’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΉχ±ξœΒΘ§‘≤![]() ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ
ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ![]() .
.
Θ®1Θ©«σ‘≤![]() ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘ®Μ·ΈΣ±ξΉΦΖΫ≥ΧΘ©ΦΑ«ζœΏ
ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘ®Μ·ΈΣ±ξΉΦΖΫ≥ΧΘ©ΦΑ«ζœΏ![]() ΒΡΤ’Ά®ΖΫ≥ΧΘΜ
ΒΡΤ’Ά®ΖΫ≥ΧΘΜ
Θ®2Θ©»τ‘≤![]() ”κ«ζœΏ
”κ«ζœΏ![]() ΒΡΙΪΙ≤œ“≥ΛΈΣ
ΒΡΙΪΙ≤œ“≥ΛΈΣ![]() Θ§«σ
Θ§«σ![]() ΒΡ÷Β.
ΒΡ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤CΖΫ≥ΧΘΚ![]() +
+![]() =1Θ®aΘΨbΘΨ0Θ©Θ§MΘ®x0 Θ§ y0Θ© «Ά÷‘≤C…œ»Έ“β“ΜΒψΘ§FΘ®cΘ§0Θ© «Ά÷‘≤ΒΡ”“ΫΙΒψΘ°
=1Θ®aΘΨbΘΨ0Θ©Θ§MΘ®x0 Θ§ y0Θ© «Ά÷‘≤C…œ»Έ“β“ΜΒψΘ§FΘ®cΘ§0Θ© «Ά÷‘≤ΒΡ”“ΫΙΒψΘ°
Θ®1Θ©»τΆ÷‘≤ΒΡάκ–Ρ¬ ΈΣeΘ§÷ΛΟς|MF|=a©¹ex0ΘΜ
Θ®2Θ©“―÷Σ≤ΜΙΐΫΙΒψFΒΡ÷±œΏl”κ‘≤x2+y2=b2œύ«–”ΎΒψQΘ§≤Δ”κΆ÷‘≤CΫΜ”ΎAΘ§BΝΫΒψΘ§«“AΘ§BΝΫΒψΕΦ‘Ύy÷αΒΡ”“≤ύΘ§»τa=2Θ§«σΓςABFΒΡ÷ή≥ΛΘ°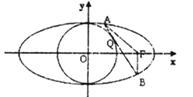
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥÷–―ßΫΪ100ΟϊΗΏ“Μ–¬…ζΖ÷≥…Υ°ΤΫœύΆ§ΒΡΦΉΓΔ““ΝΫΗωΓΑΤΫ––ΑύΓ±Θ§ΟΩΑύ50»ΥΘ°≥¬άœ Π≤…”ΟAΘ§BΝΫ÷÷≤ΜΆ§ΒΡΫΧ―ßΖΫ ΫΖ÷±π‘ΎΦΉΓΔ““ΝΫΗωΑύΦΕΫχ––ΫΧΗΡ Β―ιΘ°ΈΣΝΥΫβΫΧ―ß–ßΙϊΘ§ΤΎΡ©ΩΦ ‘ΚσΘ§≥¬άœ ΠΖ÷±π¥”ΝΫΗωΑύΦΕ÷–ΗςΥφΜζ≥ι»Γ20Οϊ―ß…ζΒΡ≥…Φ®Ϋχ––Ά≥ΦΤΘ§Ής≥ωΨΞ“ΕΆΦ»γΆΦΘ°Φ«≥…Φ®≤ΜΒΆ”Ύ90Ζ÷’ΏΈΣΓΑ≥…Φ®”≈–ψΓ±Θ°

Θ®1Θ©‘Ύ““Αύ―υ±ΨΒΡ20ΗωΗωΧε÷–Θ§¥”≤ΜΒΆ”Ύ86Ζ÷ΒΡ≥…Φ®÷–ΥφΜζ≥ι»Γ2ΗωΘ§«σ≥ι≥ωΒΡ2ΗωΨυΓΑ≥…Φ®”≈–ψΓ±ΒΡΗ≈¬ ΘΜ
Θ®2Θ©”…“‘…œΆ≥ΦΤ ΐΨίΉς≥ωΝ–ΝΣ±μΘ§≤Δ≈–ΕœΡήΖώ‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ0.1ΒΡ«ΑΧαœ¬»œΈΣΘΚΓΑ≥…Φ®”≈–ψΓ±”κΫΧ―ßΖΫ Ϋ”–ΙΊΘ°
| 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
≤ΈΩΦΙΪ ΫΘΚ![]()
![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΒς≤ιΜΦΈΗ≤Γ «Ζώ”κ…ζΜνΙφ¬…”–ΙΊΘ§‘ΎΡ≥ΒΊΕ‘![]() Οϊ
Οϊ![]() Υξ“‘…œΒΡ»ΥΫχ––ΝΥΒς≤ιΘ§ΫαΙϊ «ΘΚΜΦΈΗ≤Γ’Ώ…ζΜν≤ΜΙφ¬…ΒΡΙ≤
Υξ“‘…œΒΡ»ΥΫχ––ΝΥΒς≤ιΘ§ΫαΙϊ «ΘΚΜΦΈΗ≤Γ’Ώ…ζΜν≤ΜΙφ¬…ΒΡΙ≤![]() »ΥΘ§ΜΦΈΗ≤Γ’Ώ…ζΜνΙφ¬…ΒΡΙ≤
»ΥΘ§ΜΦΈΗ≤Γ’Ώ…ζΜνΙφ¬…ΒΡΙ≤![]() »ΥΘ§Έ¥ΜΦΈΗ≤Γ’Ώ…ζΜν≤ΜΙφ¬…ΒΡΙ≤
»ΥΘ§Έ¥ΜΦΈΗ≤Γ’Ώ…ζΜν≤ΜΙφ¬…ΒΡΙ≤![]() »ΥΘ§Έ¥ΜΦΈΗ≤Γ’Ώ…ζΜνΙφ¬…ΒΡΙ≤
»ΥΘ§Έ¥ΜΦΈΗ≤Γ’Ώ…ζΜνΙφ¬…ΒΡΙ≤![]() »Υ.
»Υ.
Θ®1Θ©ΗυΨί“‘…œ ΐΨίΝ–≥ω![]() Ν–ΝΣ±μΘΜ
Ν–ΝΣ±μΘΜ
Θ®2Θ©ΡήΖώ‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ![]() ΒΡ«ΑΧαœ¬»œΈΣΓΑ
ΒΡ«ΑΧαœ¬»œΈΣΓΑ![]() Υξ“‘…œΒΡ»ΥΜΦΈΗ≤Γ”κΖώΚΆ…ζΜνΙφ¬…”–ΙΊœΒΘΩΓ±
Υξ“‘…œΒΡ»ΥΜΦΈΗ≤Γ”κΖώΚΆ…ζΜνΙφ¬…”–ΙΊœΒΘΩΓ±
ΗΫΘΚ![]() Θ§Τδ÷–
Θ§Τδ÷–![]() .
.
|
|
|
|
|
|
|
|
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Ρ≥ΈέΥ°¥Πάμ≥ß“Σ‘Ύ“ΜΗωΨΊ–ΈΈέΥ°¥Πάμ≥Ί(ABCD)ΒΡ≥ΊΒΉΥ°ΤΫΤΧ…ηΈέΥ°ΨΜΜ·ΙήΒά(ΙήΒάΙΙ≥…RtΓςFHEΘ§H «÷±Ϋ«œνΒψ)ά¥¥ΠάμΈέΥ°Θ°ΙήΒά‘Ϋ≥ΛΘ§ΈέΥ°ΨΜΜ·–ßΙϊ‘ΫΚΟΘ°…ηΦΤ“Σ«σΙήΒάΒΡΫ”ΩΎH «ABΒΡ÷–ΒψΘ§EΘ§FΖ÷±π¬δ‘ΎœΏΕΈBCΘ§AD…œΘ°“―÷ΣABΘΫ20ΟΉΘ§ADΘΫ![]() ΟΉΘ§Φ«ΓœBHEΘΫ
ΟΉΘ§Φ«ΓœBHEΘΫ![]() Θ°
Θ°

Θ®1Θ© ‘ΫΪΈέΥ°ΨΜΜ·ΙήΒάΒΡ≥ΛΕ»L±μ ΨΈΣ![]() ΒΡΚ· ΐΘ§≤Δ–¥≥ωΕ®“ε”ρΘΜ
ΒΡΚ· ΐΘ§≤Δ–¥≥ωΕ®“ε”ρΘΜ
Θ®2Θ©Β±![]() »ΓΚΈ÷Β ±Θ§ΈέΥ°ΨΜΜ·–ßΙϊΉνΚΟΘΩ≤Δ«σ≥ω¥Υ ±ΙήΒάΒΡ≥ΛΕ»LΘ°
»ΓΚΈ÷Β ±Θ§ΈέΥ°ΨΜΜ·–ßΙϊΉνΚΟΘΩ≤Δ«σ≥ω¥Υ ±ΙήΒάΒΡ≥ΛΕ»LΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com