Question

【题目】在平面直角坐标系中，以原点为极点，x轴的非负半轴为极轴，并在两坐标系中取相同的长度单位，若直线l的极坐标方程是ρsin（θ+ ）=2 ，且点P是曲线C： （θ为参数）上的一个动点．
（Ⅰ）将直线l的方程化为直角坐标方程；
（Ⅱ）求点P到直线l的距离的最大值与最小值．

Answer 1

【答案】解：（Ⅰ）∵直线l的极坐标方程是ρsin（θ+ ）=2 ，

∴ ，

∴ρsinθ+ρcosθ=4，

由ρsinθ=y，ρcosθ=x，得x+y=4．

∴直线l的直角坐标方程为x+y=4．

（Ⅱ）∵点P是曲线C： （θ为参数）上的一个动点，

∴P（ ），

点P到直线l的距离d= = ，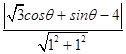

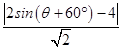∴点P到直线l的距离的最大值dmax= =3 ，

点P到直线l的距离的最小值dmin= = ．

【解析】（Ⅰ）直线l的极坐标方程转化为ρsinθ+ρcosθ=4，由ρsinθ=y，ρcosθ=x，能求出直线l的直角坐标方程．（Ⅱ）由题意P（ ），从而点P到直线l的距离d= = ，由此能求出点P到直线l的距离的最大值与最小值．