
 ⊥平面AMN; (6分)
⊥平面AMN; (6分)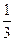
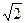 ,E是MN中点,可得AE⊥MN,CE⊥MN,又AE∩EC=E从而MN⊥平面AEC;
,E是MN中点,可得AE⊥MN,CE⊥MN,又AE∩EC=E从而MN⊥平面AEC;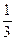 。
。
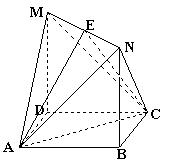
 MD⊥DA,MD⊥DC,又底面ABCD为正方形
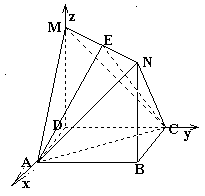
MD⊥DA,MD⊥DC,又底面ABCD为正方形 DA⊥DC,故以点D为坐标原点,DA为x轴,DC为y轴,DM为z轴,如图建立空间直角坐标系。
DA⊥DC,故以点D为坐标原点,DA为x轴,DC为y轴,DM为z轴,如图建立空间直角坐标系。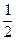 ,
,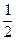 ,1) ……3分
,1) ……3分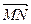 ·
·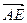 =…=0
=…=0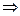 MN⊥AE;
MN⊥AE;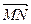 ·
·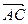 =…=0
=…=0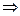 MN⊥AC
MN⊥AC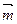 =(1,y,z),平面ANC的法向量为
=(1,y,z),平面ANC的法向量为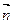 =(1,m,n) 则由
=(1,m,n) 则由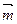 ⊥
⊥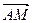 ,
,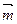 ⊥
⊥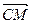
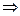
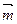 ·
·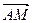 =0,
=0,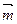 ·
·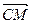 =0,代入坐标解得
=0,代入坐标解得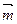 =(1,1,1)---9分
=(1,1,1)---9分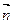 ⊥
⊥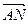 ,
,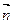 ⊥
⊥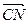
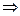
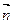 ·
·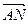 =0,
=0,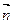 ·
·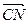 =0,代入坐标运算得
=0,代入坐标运算得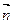 =(1,1,-1)--11分
=(1,1,-1)--11分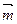 ,
,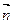 >=
>=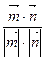 =
=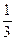 -------12分
-------12分

 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
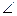 BCF=
BCF=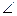 CEF=
CEF=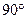 ,AD=
,AD=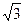 ,EF=2.
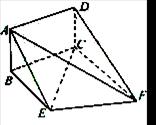
,EF=2.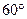 .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
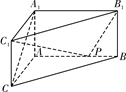
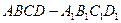 的棱长为
的棱长为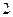 ,
,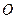 是
是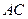 与
与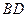 的交点,
的交点,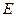 是
是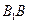 上一点,且
上一点,且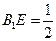 .
.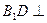 平面
平面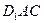 ; (2)求异面直线
; (2)求异面直线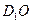 与
与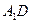 所成角的余弦值;
所成角的余弦值;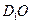 与平面
与平面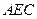 所成角的正弦值.
所成角的正弦值.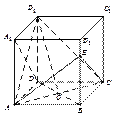
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
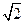 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。 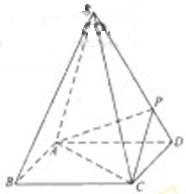
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
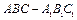 中,
中,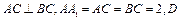 、
、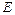 、
、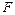 分别是
分别是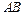 、
、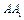 、
、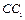 的中点,
的中点,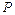 是
是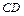 上的点.
上的点.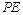 与平面
与平面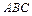 所成角的正切值的最大值;
所成角的正切值的最大值;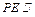 平面
平面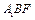 ;
;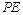 与平面
与平面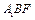 的距离.
的距离.
|

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com