
(1)确定椭圆的长轴的范围,并求AB的方程;
(2)是否存在这样的实数λ,使得以AB为直径的圆恰好经过原点?如果有,求出λ,如不存在,请说明理由.
解:(1)设A(x1,y1),B(x2,y2),∵A、B两点在椭圆上,
∴3x12+y12=λ,①
3x22+y22=λ,②
两式相减得3(x1-x2)(x1+x2)+(y1+y2)(y1-y2)=0.
∵N(1,3)为AB的中点,∴x1+x2=2,y1+y2=6,得kAB=![]() =-1,
=-1,
这时AB的方程为:y=-x+4.
联立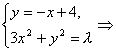 4x2-8x+16-λ=0.
4x2-8x+16-λ=0.
∴Δ=82-4×4×(16-λ)>0,∴λ>12,∴长轴2a=![]() .
.
另解:∵AB与椭圆有两个公共点,且N为AB中点,∴N(1,3)必须在椭圆的内部,
∴3+32<λ,∴λ>12.
(2)设满足条件的λ存在,
由(1)得4x2-8x-λ+16=0得x1+x2=2,x1·x2=![]() ,
,
∴y1·y2=x1x2-4(x1+x2)+16,由题意知![]() =0.
=0.
即x1·x2+y1·y2=0,∴x1x2-2(x1+x2)+8=0.
∴![]() -4+8=0,得λ=32>12,∴存在λ=32满足题设要求.
-4+8=0,得λ=32>12,∴存在λ=32满足题设要求.
另解:联立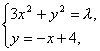 分别消去x、y,
分别消去x、y,
得4x2-8x-λ+16=0,①
4y2-24y+48-λ=0,②
①+②得2x2+2y2-4x-12y+32-λ=0.
即为以AB为直径的圆的方程.∵圆过原点,∴λ=32为所求.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:期末题 题型:解答题
查看答案和解析>>
科目:高中数学 来源:模拟题 题型:解答题
查看答案和解析>>
科目:高中数学 来源:湖北 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com