
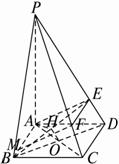
(1)证明MF是异面直线AB与PC的公垂线;
(2)若PA=3AB,求直线AC与平面EAM所成角的正弦值.
(1)证明:因PA⊥底面ABCD,有PA⊥AB.
又知AB⊥AD,故AB⊥面PAD,推得BA⊥AE.
又AM∥CD∥EF,且AM=EF,
可得AEFM是矩形,故AM⊥MF.
又因为AE⊥PD,AE⊥CD,故AE⊥面PCD.
而MF∥AE,得MF⊥面PCD.故MF⊥PC.
因此MF是AB与PC的公垂线.
(2)解:如下图,连结BD交AC于O点,连结BE,过O作BE的垂线OH,垂足H在BE上,易知PD⊥面MAE,故DE⊥BE.
又OH⊥BE,故OH∥DE.

因此OH⊥平面MAE.
连结AH,则∠HAO是所要求的直线AC与平面MAE所成的角.
设AB=a,
则PA=![]() AC=
AC=![]() a.
a.
因Rt△ADE∽Rt△PDA,
故ED=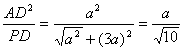 ,OH=
,OH=![]() ED=
ED=![]() ,
,
从而在Rt△AHO中,sinHAO=![]() .
.
点评:求直线和平面所成的角时,应注意的问题是:(1)先判断直线和平面的位置关系;(2)当直线和平面斜交时,常有以下步骤:①作——作出或找到斜线与射影所成的角;②证——论证所作或找到的角为所求的角;③算——常用解三角形的方法求角;④结论——点明斜线和平面所成的角的值.


科目:高中数学 来源: 题型:
 由两个完全相同的正四棱锥组合而成的空间几何体的正(主)视图、侧(左)视图、俯视图相同如下图所示,其中视图中四边形ABCD是边长为1的正方形,则该几何体的表面积为( )
由两个完全相同的正四棱锥组合而成的空间几何体的正(主)视图、侧(左)视图、俯视图相同如下图所示,其中视图中四边形ABCD是边长为1的正方形,则该几何体的表面积为( )A、
| ||
B、2
| ||
C、3
| ||
D、4
|
查看答案和解析>>
科目:高中数学 来源:2007年普通高等学校招生全国统一考试、文科数学(湖南卷) 题型:013
如下图,在正四棱柱ABCD-A1B1C1D1中,E、F分别是AB1、BC1的中点,则以下结论中不成立的是
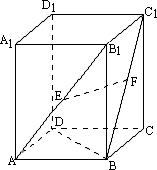
A.EF与BB1垂直
B.EF与BD垂直
C.EF与CD异面
D.EF与A1C1异面
查看答案和解析>>
科目:高中数学 来源: 题型:
A.0条 B.1条 C.2条 D.无数条
查看答案和解析>>
科目:高中数学 来源: 题型:
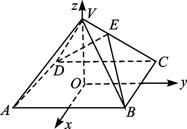
(1)求cos〈![]() ,
,![]() 〉;
〉;
(2)记面BCV为α,面DCV为β,若∠BED是二面角α-VC-β的平面角,求∠BED.
查看答案和解析>>
科目:高中数学 来源: 题型:
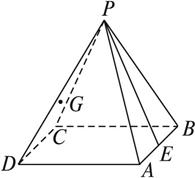
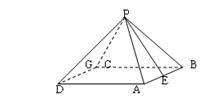
如下图,在正四棱锥P-ABCD中,PA=![]() AB,E是AB的中点,G是△PCD的重心,则在平面PCD内过G点且与PE垂直的直线有( )
AB,E是AB的中点,G是△PCD的重心,则在平面PCD内过G点且与PE垂直的直线有( )
A、0条 B、1条 C、2条 D、无数条
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com