
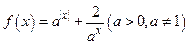 ,
,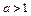 ,且关于
,且关于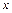 的方程
的方程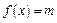 有两个不同的正数解,求实数
有两个不同的正数解,求实数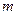 的取值范围;
的取值范围;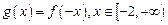 ,
,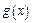 满足如下性质:若存在最大(小)值,则最大(小)值与
满足如下性质:若存在最大(小)值,则最大(小)值与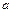 无关.试求
无关.试求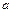 的取值范围.
的取值范围.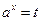 ,
,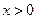 ,因为
,因为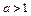 ,所以
,所以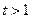 ,所以关于
,所以关于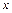 的方程
的方程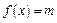 有两个不同的正数解等价于关于
有两个不同的正数解等价于关于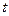 的方程
的方程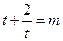 有相异的且均大于1的两根,即关于
有相异的且均大于1的两根,即关于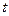 的方程
的方程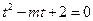 有相异的且均大于1的两根,……………………………………………………2分
有相异的且均大于1的两根,……………………………………………………2分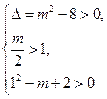 ,…………………………………………………………………4分
,…………………………………………………………………4分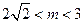 ,故实数
,故实数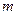 的取值范围为区间
的取值范围为区间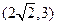 .……………………………6分
.……………………………6分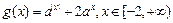
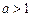 时,
时,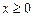 时,
时,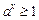 ,
,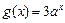 ,所以
,所以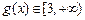 ,
,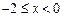 时,
时,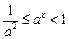
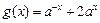 ,所以
,所以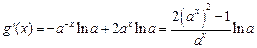 ……8分
……8分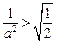 即
即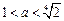 时,对
时,对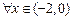 ,
,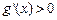 ,所以
,所以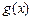 在
在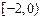 上递增,
上递增,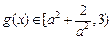 ,综合a) b)
,综合a) b)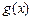 有最小值为
有最小值为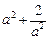 与a有关,不符合……10分
与a有关,不符合……10分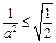 即
即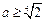 时,由
时,由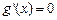 得
得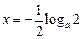 ,且当
,且当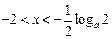 时,
时,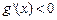 ,当
,当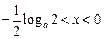 时,
时,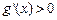 ,所以
,所以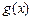 在
在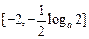 上递减,在
上递减,在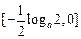 上递增,所以
上递增,所以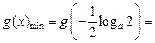
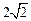 ,综合a) b)
,综合a) b) 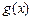 有最小值为
有最小值为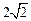 与a无关,符合要求.………12分
与a无关,符合要求.………12分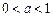 时,
时,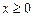 时,
时,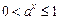 ,
,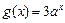 ,所以
,所以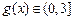
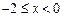 时,
时,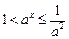 ,
,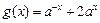 ,
,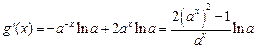
 ,
,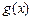 在
在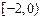 上递减,
上递减,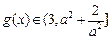 ,综合a) b)
,综合a) b) 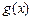 有最大值为
有最大值为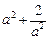 与a有关,不符合………14分
与a有关,不符合………14分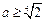 .………………………………………………16分
.………………………………………………16分

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源:不详 题型:解答题
 元购进一批商品,若该商品零售价定为
元购进一批商品,若该商品零售价定为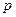 元,则销售量
元,则销售量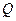 (单位:件)与零售价
(单位:件)与零售价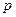 (单位:元)有如下关系:
(单位:元)有如下关系: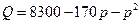 ,问该商品零售价定为多少时利润
,问该商品零售价定为多少时利润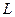 最大,并求出最大利润(利润
最大,并求出最大利润(利润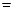 销售收入
销售收入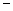 进货支出)
进货支出)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
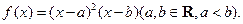
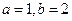 时,求曲线
时,求曲线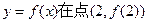 处的切线方程;
处的切线方程;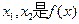 的两个极值点,
的两个极值点,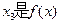 的一个零点,且
的一个零点,且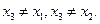 证明:存在实数
证明:存在实数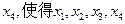 按照某种顺序排列后构成等差数列,并求
按照某种顺序排列后构成等差数列,并求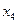 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com