
设数列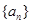 的前
的前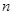 项和
项和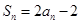 .数列
.数列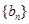 满足:
满足: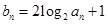 .
.
(1)求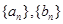 的通项
的通项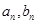 .并比较
.并比较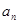 与
与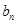 的大小;
的大小;
(2)求证: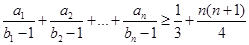 .
.
(1) 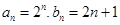 .
.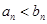 。
。
(2)首先我们证明当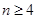 时,
时,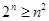
事实上,记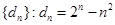 . ∵
. ∵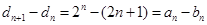
由(1)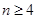 时,
时,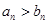 . ∴
. ∴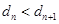 . 而
. 而 .
.
∴当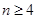 时,
时,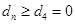 即
即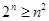 . 从而
. 从而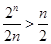 .
.
解析试题分析:(1)由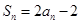 ① 当
① 当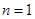 时,
时,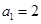 .
.
当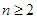 时,
时,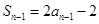 ② 由①-②有
② 由①-②有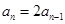 . ∵
. ∵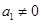
∴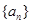 是2为首项,2为公比的等比数列. 从而
是2为首项,2为公比的等比数列. 从而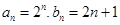 .
.
设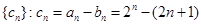
∵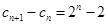 . ∴
. ∴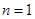 时,
时, 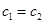 . 当
. 当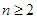 时,
时,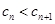
又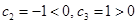 . ∴当
. ∴当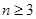 时,
时, 即
即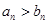 .
.
当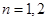 时,显见
时,显见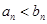
(2)首先我们证明当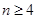 时,
时,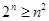
事实上,记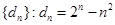 . ∵
. ∵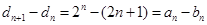
由(1)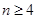 时,
时,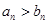 . ∴
. ∴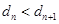 . 而
. 而 .
.
∴当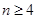 时,
时,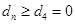 即
即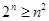 . 从而
. 从而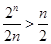 .
.
当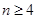 时,不等式的
时,不等式的
左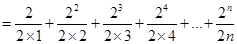

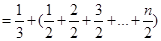
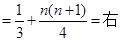
容易验证当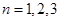 时,不等式也显然成立.
时,不等式也显然成立.
从而对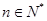 ,所证不等式均成立.
,所证不等式均成立.
考点:本题主要考查等差数列、等比数列的通项公式,“放缩法”,不等式的证明。
点评:典型题,确定数列的通项公式,一般地,通过布列方程组,求相关元素。涉及数列不等式的证明问题,“放缩、求和、证明”和“数学归纳法”等证明方法,能拓宽学生的视野。


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:解答题
如图所示,流程图给出了无穷等差整数列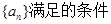 ,
,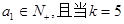 时,输出的
时,输出的 时,输出的
时,输出的 (其中d为公差)
(其中d为公差)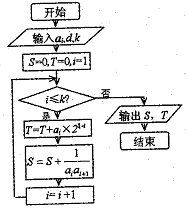
(I)求数列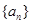 的通项公式;
的通项公式;
(II)是否存在最小的正数m,使得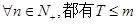 成立?若存在,求出m的值,若不存在,请说明理由。
成立?若存在,求出m的值,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在数列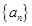 中,
中,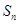 是数列
是数列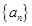 前
前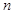 项和,
项和,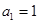 ,当
,当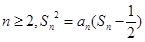
(1)证明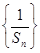 为等差数列;;
为等差数列;;
(2)设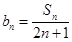 求数列
求数列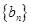 的前
的前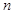 项和
项和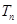 ;
;
(3)是否存在自然数m,使得对任意自然数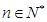 ,都有
,都有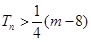 成立?若存在,
成立?若存在,
求出m 的最大值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
数列{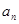 }中,a1=3,
}中,a1=3,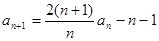 ,
,
(1)求a1、a2、a3、a4;
(2)用合情推理猜测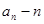 关于n的表达式(不用证明);
关于n的表达式(不用证明);
(3)用合情推理猜测{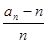 }是什么类型的数列并证明;
}是什么类型的数列并证明;
(4)求{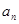 }的前n项的和。
}的前n项的和。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com