
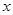 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线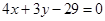 相切.
相切.
 与圆相交于
与圆相交于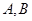 两点,求实数
两点,求实数 的取值范围;
的取值范围; ,使得弦
,使得弦 的垂直平分线
的垂直平分线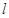 过点
过点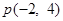 ,
,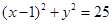 ;(2)
;(2)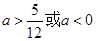 ;(3)
;(3)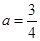
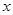 轴,可设圆心为
轴,可设圆心为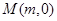 ,又直线
,又直线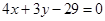 与圆相切,∴圆心到直线的距离
与圆相切,∴圆心到直线的距离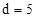 ,列式求
,列式求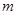 ,则圆的标准方程可求;(2)因为直线
,则圆的标准方程可求;(2)因为直线
 与圆相交于
与圆相交于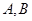 两点,则
两点,则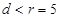 ,解不等式可求实数
,解不等式可求实数 的取值范围;(3)首先根据垂直关系得
的取值范围;(3)首先根据垂直关系得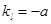 ,又直线
,又直线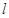 过点
过点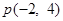 ,根据直线的点斜式方程写出
,根据直线的点斜式方程写出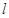 的方程为
的方程为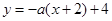 ,由垂径定理可知,弦
,由垂径定理可知,弦 的垂直平分线必过圆心,将圆心
的垂直平分线必过圆心,将圆心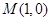 代入,可求
代入,可求 的值,再检验直线是否圆相交于两点.
的值,再检验直线是否圆相交于两点.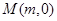 (m∈Z),由于圆与直线4x+3y-29=0相切,且半径为5,∴
(m∈Z),由于圆与直线4x+3y-29=0相切,且半径为5,∴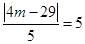 即|4m-29|=25,即4m-29=25或4m-29=-25,解得
即|4m-29|=25,即4m-29=25或4m-29=-25,解得 ,或
,或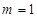 ,因为m为整数,故m=1,故所求的圆的方程是
,因为m为整数,故m=1,故所求的圆的方程是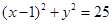 ;
;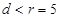 ,
,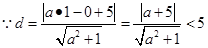
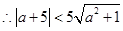
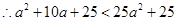 ,
,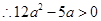 即:
即: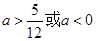 ;
;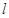 斜率为
斜率为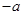 ,
,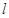 的方程为
的方程为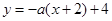 ,即
,即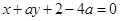 ,由于直线
,由于直线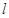 垂直平分弦AB,故圆心M(1,0)必在
垂直平分弦AB,故圆心M(1,0)必在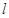 ,所以1+0+2-4a=0,解得
,所以1+0+2-4a=0,解得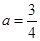 ,
,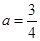 ,直线ax-y+5=0与圆有两个交点,故存在实数
,直线ax-y+5=0与圆有两个交点,故存在实数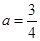 ,使得过点P(-2,4)的直线
,使得过点P(-2,4)的直线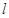 垂直平分弦AB.
垂直平分弦AB.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com