
【题目】平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的离心率为
的离心率为![]() ,焦点为
,焦点为![]() 、
、![]() ,直线
,直线![]() 经过焦点
经过焦点![]() ,并与
,并与![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)在![]() 上是否存在
上是否存在![]() 、
、![]() 两点,满足
两点,满足![]() //
//![]() ,
,![]() ?若存在,求直线
?若存在,求直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
【答案】(1)![]() (2)不存在满足条件的直线
(2)不存在满足条件的直线
【解析】
试题(1)由椭圆几何性质求得![]() 得到椭圆方程;(2)首先设出CD直线
得到椭圆方程;(2)首先设出CD直线![]() ,与椭圆联立整理为
,与椭圆联立整理为![]() 的二次方程,找到根与系数的关系,由已知
的二次方程,找到根与系数的关系,由已知![]() 转化出
转化出![]() ,代入点的坐标整理求的
,代入点的坐标整理求的![]() 的值,最后要注意验证二次方程中
的值,最后要注意验证二次方程中![]() 是否成立
是否成立
试题解析:(1)依题意![]() ,
,![]() ,由
,由![]() 得
得![]()
![]() ,椭圆的方程为
,椭圆的方程为![]()
(2)(方法一)若存在满足条件的直线![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
设直线![]() 的方程为
的方程为![]()
由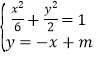 ……6分,得
……6分,得![]() ,
,
![]() (*)
(*)
设![]() ,
,![]() ,则
,则![]() ,
,![]()
若线段![]() 的中点为
的中点为![]() ,则
,则![]() 即
即![]()
由已知![]() ,则
,则![]() ,
,![]() ,
,![]() ,由
,由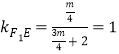 ,解得
,解得![]()
![]() 时,
时,![]() ,与(*)矛盾,∴不存在满足条件的直线
,与(*)矛盾,∴不存在满足条件的直线![]()
(方法二)假设存在![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() ,则
,则![]() ,
,![]() 由
由 两式相减得
两式相减得
![]() 代入、化简得:
代入、化简得:![]() ①
①
由已知![]() ,则
,则![]() ,
,![]() 由
由![]() 得,
得,![]() ② 由①②解得
② 由①②解得![]() ,即
,即![]() 直线CD的方程为:
直线CD的方程为:![]()
联立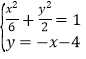 得
得![]() ,∵
,∵![]() ,方程组无解,
,方程组无解,
∴不存在满足条件的直线![]()


科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”, 《中华人民共和国道路交通安全法》第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员“礼让斑马线”行为统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
违章驾驶员人数 | 120 | 105 | 100 | 90 | 85 |
(1)请利用所给数据求违章人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)预测该路口9月份的不“礼让斑马线”违章驾驶员人数.
参考公式:  ,
, ![]() .
.
参考数据: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
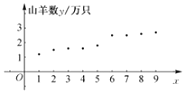
【题目】某县畜牧技术员张三和李四9年来一直对该县山羊养殖业的规模进行跟踪调查,张三提供了该县某山羊养殖场年养殖数量![]() 单位:万只
单位:万只![]() 与相应年份
与相应年份![]() 序号
序号![]() 的数据表和散点图
的数据表和散点图![]() 如图所示
如图所示![]() ,根据散点图,发现y与x有较强的线性相关关系,李四提供了该县山羊养殖场的个数
,根据散点图,发现y与x有较强的线性相关关系,李四提供了该县山羊养殖场的个数![]() 单位:个
单位:个![]() 关于x的回归方程
关于x的回归方程![]() .
.
年份序号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
年养殖山羊 |
|
|
|
|
|
|
|
|
|
![]() 根据表中的数据和所给统计量,求y关于x的线性回归方程
根据表中的数据和所给统计量,求y关于x的线性回归方程![]() 参考统计量:
参考统计量:![]() ,
,![]() ;
;
![]() 试估计:
试估计:![]() 该县第一年养殖山羊多少万只
该县第一年养殖山羊多少万只
![]() 到第几年,该县山羊养殖的数量与第一年相比缩小了?
到第几年,该县山羊养殖的数量与第一年相比缩小了?
附:对于一组数据![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为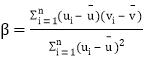 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个关于圆锥曲线的命题:
①设A,B是两个定点,![]() 为非零常数,若
为非零常数,若![]() ,则P的轨迹是双曲线;
,则P的轨迹是双曲线;
②过定圆C上一定点A作圆的弦AB,O为原点,若向量![]() .则动点P的轨迹是椭圆;
.则动点P的轨迹是椭圆;
③方程![]() 的两根可以分别作为椭圆和双曲线的离心率;
的两根可以分别作为椭圆和双曲线的离心率;
④双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点.
有相同的焦点.
其中正确命题的序号为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com