
设为a,b,c正数,记d为![]() ,
, ![]() ,
, ![]() 中的最小数.
中的最小数.
(1)求证:存在λ(0<λ<1=,使得d≤![]() ;......(*)
;......(*)
(2)求出使不等式(*)成立的最小正数λ并给予证明.
科目:高中数学 来源:山东省济南外国语学校2010届高三上学期质量检测 题型:选择题
设函数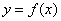 在
在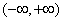 内有定义,对于给定的正数K,定义函数
内有定义,对于给定的正数K,定义函数 ,取函数
,取函数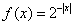 ,当K=
,当K= 时,函数
时,函数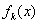 的单调递增区间为
的单调递增区间为
A. 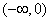 B
.
B
. C .
C . 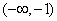 D.
D.
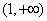
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com