
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1,a32=9a2a6 .
(1)求数列{an}的通项公式;
(2)设bn=|10+2log3an|,求数列{bn}的前n项和Sn .
【答案】
(1)解:设等比数列{an}的各项均为正数,且公比为q(q>0),
由2a1+3a2=1,a32=9a2a6,可得:
2a1+3qa1=1,(a1q2)2=9a12q6,
解得a1=q= ![]() ,
,
可得数列{an}的通项公式为an=a1qn﹣1=( ![]() )n;
)n;
(2)解:bn=|10+2log3an|=|10+2log33﹣n|=|10﹣2n|,
当1≤n≤5时,bn=10﹣2n,
前n项和Sn= ![]() (8+10﹣2n)n=9n﹣n2;
(8+10﹣2n)n=9n﹣n2;
当n>5时,前n项和Sn=8+6+4+2+0+2+4+6+…+2n﹣10
=20+ ![]() (2+2n﹣10)(n﹣5)=n2﹣9n+40.
(2+2n﹣10)(n﹣5)=n2﹣9n+40.
综上可得,前n项和Sn= ![]() .
.
【解析】(1)设等比数列{an}的各项均为正数,且公比为q(q>0),运用等比数列的通项公式,解方程可得首项和公比为 ![]() ,运用等比数列的通项公式即可得到所求;(2)求得bn=|10+2log3an|=|10+2log33﹣n|=|10﹣2n|,讨论当1≤n≤5时,当n>5时,运用等差数列的求和公式,计算即可得到所求和.
,运用等比数列的通项公式即可得到所求;(2)求得bn=|10+2log3an|=|10+2log33﹣n|=|10﹣2n|,讨论当1≤n≤5时,当n>5时,运用等差数列的求和公式,计算即可得到所求和.
【考点精析】掌握等比数列的通项公式(及其变式)和数列的前n项和是解答本题的根本,需要知道通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系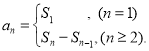 .
.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知圆心在x轴上、半径为2的圆C位于y轴右侧,且与直线 ![]() 相切.
相切.
(1)求圆C的方程;
(2)在圆C上,是否存在点M(m,n),使得直线l:mx+ny=1与圆O:x2+y2=1相交于不同的两点A,B,且△OAB的面积最大?若存在,求出点M的坐标及对应的△OAB的面积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点为极点,以
为参数),以原点为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)![]() 为曲线
为曲线![]() 上任一点,过点
上任一点,过点![]() 作曲线
作曲线![]() 的切线
的切线![]() (
(![]() 为切点),求
为切点),求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某特色餐馆开通了美团外卖服务,在一周内的某特色菜外卖份数![]() (份)与收入
(份)与收入![]() (元)之间有如下的对应数据:
(元)之间有如下的对应数据:
外卖份数 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计外卖份数为12份时,收入为多少元.
注:①参考公式:线性回归方程系数公式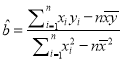 ,
, ![]() ;
;
②参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 满足:(1)截
满足:(1)截![]() 轴所得弦长为2;(2)被
轴所得弦长为2;(2)被![]() 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为![]() .在满足条件(1)、(2)的所有圆中,圆心到直线
.在满足条件(1)、(2)的所有圆中,圆心到直线![]() 的距离最小的圆的方程为__________.
的距离最小的圆的方程为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁﹣18岁的男生体重(kg),得到频率分布直方图如图.根据图可得这100名学生中体重在〔56.5,64.5〕的学生人数是( ) 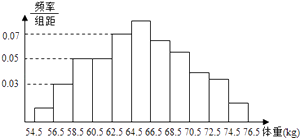
A.20
B.30
C.40
D.50
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com