解:(1)已知函数f(x)=
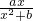
,
∴
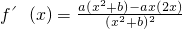
.…(2分)
又函数f(x)在x=1处取得极值2,
∴
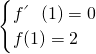
,
即


,
∴
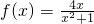
.…(4分)
(2)由
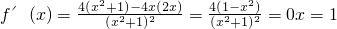
.…(5分)
| x | (-∞,-1) | -1 | (-1,1) | 1 | (1,+∞) |
| f'(x) | - | 0 | + | 0 | - |
| f(x) | 单调递减 | 极小值-2 | 单调递增 | 极大值2 | 单调递减 |
所以
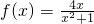
的单调增区间为[-1,1].…(7分)
若(m,2m+1)为函数f(x)的单调增区间,
则有

,
解得-1<m≤0.
即m∈(-1,0]时,(m,2m+1)为函数f(x)的单调增区间.…(9分)
(3)分两种情况讨论如下:
①当m≤-1时,由(2)得f(x)在(-∞,m]单调递减,
要使f(x)≥m恒成立,
必须
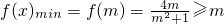
,…(10分)
因为m≤-1,
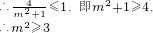
∴
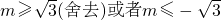
…(12分)
②当-1<m<1时,
由(2)得f(x)在(-∞,-1)单调递减,在(-1,m]单调递增,
要使f(x)≥m恒成立,
必须f(x)
min=f(-1)=-2≥m,
故此时不存在这样的m值.
综合①②得:满足条件的m的取值范围是
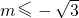
. …(14分)
分析:(1)由f(x)=
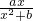
,知
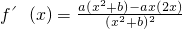
.由函数f(x)在x=1处取得极值2,得
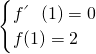
由此能求出
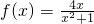
.
(2)由
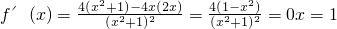
.列表讨论得到
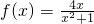
的单调增区间为[-1,1].由此能求出函数f(x)在区间(m,2m+1)上单调递增时实数m的条件.
(3)当m≤-1时,由(2)得f(x)在(-∞,m]单调递减,要使f(x)≥m恒成立,必须
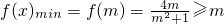
;当-1<m<1时,由(2)得f(x)在(-∞,-1)单调递减,在(-1,m]单调递增,
要使f(x)≥m恒成立,必须f(x)
min=f(-1)=-2≥m.由此能求出满足条件的m的取值范围.
点评:本题考查函数解析式的求法,导数的应用,考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,是高考的重点,对数学思维的要求比较高,要求学生理解“存在”、“恒成立”,以及运用一般与特殊的关系进行否定,本题有一定的探索性,难度大,易出错.

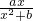 在x=1处取得极值2.
在x=1处取得极值2.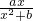 ,
,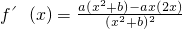 .…(2分)
.…(2分)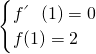 ,
,
 ,
,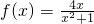 .…(4分)
.…(4分)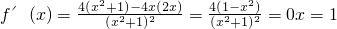 .…(5分)
.…(5分)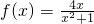 的单调增区间为[-1,1].…(7分)
的单调增区间为[-1,1].…(7分) ,
,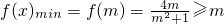 ,…(10分)
,…(10分)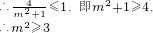
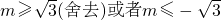 …(12分)
…(12分)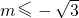 . …(14分)
. …(14分)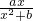 ,知
,知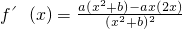 .由函数f(x)在x=1处取得极值2,得
.由函数f(x)在x=1处取得极值2,得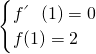 由此能求出
由此能求出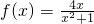 .
.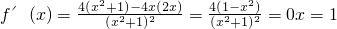 .列表讨论得到
.列表讨论得到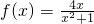 的单调增区间为[-1,1].由此能求出函数f(x)在区间(m,2m+1)上单调递增时实数m的条件.
的单调增区间为[-1,1].由此能求出函数f(x)在区间(m,2m+1)上单调递增时实数m的条件.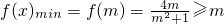 ;当-1<m<1时,由(2)得f(x)在(-∞,-1)单调递减,在(-1,m]单调递增,
;当-1<m<1时,由(2)得f(x)在(-∞,-1)单调递减,在(-1,m]单调递增,
