已知动圆M与直线x=-2相切,且与定圆C:(x-3)2+y2=1外切.
(Ⅰ)求动圆圆心M的轨迹方程;
(Ⅱ)若正△OAB的三个顶点都在点M的轨迹上(O为坐标原点),求该正三角形的边长.
分析:(Ⅰ)动圆M与直线x=-2相切,且与定圆C:(x-3)
2+y
2=1,可以看到动圆的圆心M到C(3,0)的距离与到直线x=-3的距离相等,由抛物线的定义知,点M的轨迹是抛物线,由此易得轨迹方程;
(Ⅱ)正△OAB的三个顶点都在点M的轨迹上(O为坐标原点),此正三角形必有一个顶点是抛物线的顶点,另两个顶点的连线垂直于抛物线的对称轴,由此易得过原点的两边所在直线y=
y=±x,与点M的轨迹方程联立,解出交点的坐标,即可求得正三角形的边长.
解答:解:(Ⅰ)由题意动圆M与直线x=-2相切,且与定圆C:(x-3)
2+y
2=1外切
∴动点M到C(3,0)的距离与到直线x=-3的距离相等
由抛物线的定义知,点M的轨迹是以C(3,0)为焦点直线x=-3为准线的抛物线
故所求M的轨迹方程为y
2=12x
(Ⅱ)由题意此正三角形必有一个顶点是抛物线的顶点,另两个顶点的连线垂直于抛物线的对称轴,可设过原点的两边所在的直线方程为
y=±x,
∴
?yA=12∴正△OAB的边长
AB=2yA=24 点评:本题考查轨迹方程,熟记抛物线的定义是求解本题的关键,由定义法求轨迹的方程是近几年高考的热点,要注意掌握高中数学中所学的几个重要定义,如圆锥曲线的定义,圆的定义等,第二小问的求解,关键是理解抛物线的对称性,从而得出此正三角的位置特征,借助这一特征求出正三角的面积



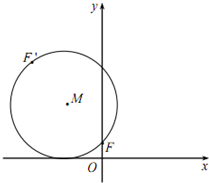 (2012•深圳二模)如图,已知动圆M过定点F(0,1)且与x轴相切,点F关于圆心M的对称点为F′,动点F′的轨迹为C.
(2012•深圳二模)如图,已知动圆M过定点F(0,1)且与x轴相切,点F关于圆心M的对称点为F′,动点F′的轨迹为C.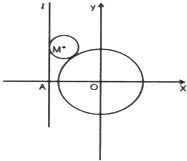 已知直线l:x=m(m<-2)与x轴交于A点,动圆M与直线l相切,并且和圆O:x2+y2=4相外切.
已知直线l:x=m(m<-2)与x轴交于A点,动圆M与直线l相切,并且和圆O:x2+y2=4相外切.