设数组A:{a1,a2,…,an}与数组B:{b1,b2,…,bn},A与B中的元素不完全相同,分别从A、B中的n个元素中任取m(m≤n)个元素作和,各得Cnm个和.若由A得到的Cnm个和与由B得到的Cnm个和恰好完全相同,则称数组A与B是n元中取m的全等和数组,简记为DHnm数组.
(1)判断数组A:{5,15,25,45}与B:{0,20,30,40}是否为DH42数组?
(2)若数组A:{a1,a2,…,an}与数组B:{b1,b2,…,bn}是DHnm数组(m≤n),求证:数组A与B一定是DHnn数组
(3)给定数组A:{a1,a2,a3,a4},其中a1≤a2≤a3≤a4,问是否存在数组B,使得数组A与B为DH42数组?若存在,则求出数组B;若不存在,请说明理由.
【答案】
分析:(1)在数组A:{5,15,25,45}中任取两个数求和,可得20,30,40,50,60,70,同样在B:{0,20,30,40}中任取两个数求和,可得20,30,40,50,60,70,故A与B为DH
42数组
(2)求证数组A与B一定是DH
nn数组,即求证a
1+a
2+…a
n=b
1+b
2+…b
n,由数组A:{a
1,a
2,…,a
n}与数组B:{b
1,b
2,…,b
n}是DH
nm数组,则由A得到的C
nm个和与由B得到的C
nm个和恰好完全相同,由此可证
(3)假设存在数组B:{b
1,b
2,b
3,b
4}(不妨设b
1≤b
2≤b
3≤b
4)与A是DH
42数组,则有a
1+a
2=b
1+b
2、a
1+a
3=b
1+b
3、a
2+a
4=b
2+b
4、a
3+a
4=b
3+b
4不妨设b
1=a
1-q则b
2=a
2+q,b
3=a
3+q,b
4=a
4-q 故

,若q=0,则存在唯一数组B,否则不存在
解答:解:(1)A中C
42个和为:20,30,40,50,60,70B中C
42个和为:20,30,40,50,60,70
∴A与B为DH
42数组
(2)证明:从A中任取m个元素作和共得C
nm个数,再将C
nm个数作和记为S,
在C
nm个数中a
1、a
2、…、a
n都分别出现了C
n-1m-1次,故S=C
n-1m-1(a
1+a
2+…a
n)
同样从B中任取m个元素作和共得C
nm个数,这些数的和为S',S'=C
n-1m-1(b
1+b
2+…b
n)
显然S=S'∴a
1+a
2+…a
n=b
1+b
2+…b
n即A与B为DH
nn数组
(3)假设存在数组B:{b
1,b
2,b
3,b
4}(不妨设b
1≤b
2≤b
3≤b
4)与A是DH
42数组,
则有a
1+a
2=b
1+b
2、a
1+a
3=b
1+b
3、a
2+a
4=b
2+b
4、a
3+a
4=b
3+b
4不妨设b
1=a
1-q则b
2=a
2+q,b
3=a
3+q,b
4=a
4-q
从而a
2+a
3=b
1+b
4(不能等于b
2+b
3否则q=0与题意不符)
故

①a
1+a
4≠a
2+a
3,则一定存在唯一数组B:{a
1-q,a
2+q,a
3+q,a
4-q}
(其中
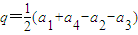
)与A是DH
42数组
②a
1+a
4=a
2+a
3,则不存在数组B与A是DH
42数组.
点评:本题考查了排列与组合的应用,属新定义型创新题,解答难度较大,解题时首先要理解题意,然后根据要求用分析法分析,综合法写出解题过程

 ,若q=0,则存在唯一数组B,否则不存在
,若q=0,则存在唯一数组B,否则不存在
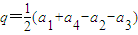 )与A是DH42数组
)与A是DH42数组
