在平面直角坐标系xOy中,点_P到定点F(-1,0)的距离的两倍和它到定直线x=-4的距离相等.
(Ⅰ)求点P的轨迹C的方程,并说明轨迹C是什么图形;
(Ⅱ)已知点Q(l,1),直线l:y=x+m(m∈R)和轨迹C相交于A、B两点,是否存在实数m,使△ABQ的面积S最大?若存在,求出m的值;若不存在,说明理由.
【答案】
分析:(I)根据直接法求轨迹方程求解;
(II)假设存在,利用直线与圆锥曲线相交弦长公式,构造三角形面积关于m的函数,利用函数求最值的方法求解即可.
解答:解:(Ⅰ)设P(x,y),根据题意,2|PF|=d.
即:2
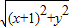
=|4+x|,
平方化简得3x
2+4y
2=12,即
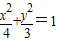
.
点P的轨迹是长轴、短轴长分别为4、2
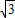
,焦点在x轴上的椭圆.
(Ⅱ)设直线L与轨迹C的交点为A(x
1,y
1),B(x
2,y
2)两点.
联立方程得:
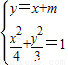
⇒7x
2+8mx+4m
2-12=0,
x
1+x
2=-
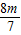
,x
1x
2=
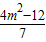
,
△=64m
2-4×7×4(m
2-3)=48(7-m
2)>0
|AB|=
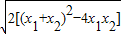
=
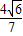
×
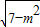
.
点Q(1,1)到L:y=x+m的距离为
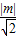
.
∴S
△=

×
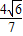
×
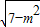
×
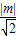
=
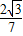
×
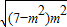
≤
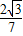
×
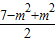
=
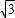
.
当且仅当7-m
2=m
2,即m=±
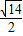
时,满足△=48(7-m
2)>0,
∴存在实数m=
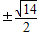
,使△ABQ的面积S最大,最大值为
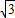
.
点评:本题考查直接法求轨迹方程及直线与圆锥曲线的位置关系.存在性问题的常见解法:假设存在,依据题设条件求出,说明存在;求不出或得出明显矛盾,说明不存在.

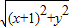 =|4+x|,
=|4+x|,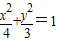 .
.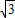 ,焦点在x轴上的椭圆.
,焦点在x轴上的椭圆.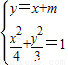 ⇒7x2+8mx+4m2-12=0,
⇒7x2+8mx+4m2-12=0,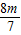 ,x1x2=
,x1x2=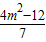 ,
,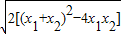 =
=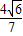 ×
×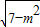 .
.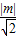 .
. ×
×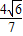 ×
×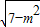 ×
×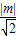 =
=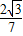 ×
×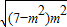 ≤
≤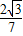 ×
×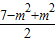 =
=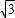 .
.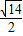 时,满足△=48(7-m2)>0,
时,满足△=48(7-m2)>0,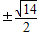 ,使△ABQ的面积S最大,最大值为
,使△ABQ的面积S最大,最大值为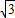 .
.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是