练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图所示空间四边形ABCD中，各边及对角线长均为2，E是AB的中点，过CE且平行于AD的平面交BD于F，则△CEF的面积为

    答案：略
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

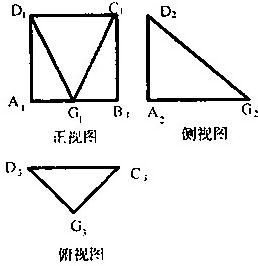    精英家教网一个空间几何体G-ABCD的三视图如图所示，其中Ai，Bi，Ci，Di，Gi（i=1，2，3）分别是A，B，C，D，G在直立、侧立、水平三个投影面内的投影．在视图中，四边形A1B2C3D4为正方形，且A1B2=2a；在侧视图中，A2D2⊥A2G2；在俯视图中，G3D3=G3C3=2
    		2a
    .
    （Ⅰ）根据三视图画出几何体的直观图，并标明A，B，C，D，G五点的位置；
    （Ⅱ）证明：平面AGD⊥平面BGC；
    （Ⅲ）求三棱锥D-ACG的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网如图所示，空间四边形ABCD中，AB=BD=AD=2，BC=CD=
    		7
    2
    ，AC=
    3
    2
    ，延长BC到E，使CE=BC，F是BD的中点，异面直线 AF、DE所成角为（　　）
    A、30°B、45°
    C、60°D、90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

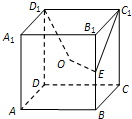    5、如图所示，O是正方体ABCD-A1B1C1D1对角线A1C与AC1的交点，E为棱BB1的中点，则空间四边形OEC1D1在正方体各面上的正投影不可能 是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，已知空间四边形的每条边和对角线长都等于a，点E、F、G分别为AB、AD、DC的中点，则a2等于（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    用平行于空间四边形ABCD一组对边AC和BD的平面截此空间四边形得一四边形MNPQ,如图所示.

    (1)四边形MNPQ是平行四边形吗?

    (2)若AC=BD,能截得菱形吗?如果能,那么如何截?

    (3)在什么情况下,可以截得一个矩形?

    (4)在什么条件下,能截得一个正方形?如果能,该怎样截?(注:只需给出满足条件的一种情形即可)

    (5)若AC=BD=a,求证:四边形MNPQ的周长为定值.

    查看答案和解析>>

    同步练习册答案