
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,求函数
时,求函数![]() 的单调递增区间;
的单调递增区间;
(3)当![]() 时,证明:
时,证明: ![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
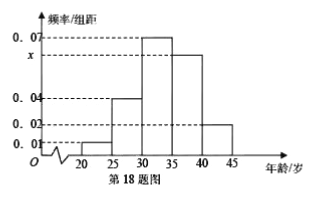
【题目】为增强市民的节能环保意识,汕头市面向全市征召义务宣传志愿者,从符合条件的 500 名志愿者中随机抽取 100 名,其年龄频率分布直方图如图所示,其中年龄分组区是:
![]() ,
,
(1)求图中![]() 的值,并根据频率分布直方图估计这 500 名志愿者中年龄在
的值,并根据频率分布直方图估计这 500 名志愿者中年龄在![]() 岁的人数;
岁的人数;
(2)在抽出的 100 名志愿者中按年龄采用分层抽样的方法抽取 10 名参加人民广场的宣传活动,再从这 10 名志愿者中选取 3 名担任主要负责人.记这 3 名志愿者中“年龄低于 35 岁”的人数为 ![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在吸烟与患肺癌这两个分类变量的独立性检验的计算中,下列说法正确的是( )
A. 若![]() 的观测值为
的观测值为![]() ,在犯错误的概率不超过
,在犯错误的概率不超过![]() 的前提下认为吸烟与患肺癌有关系,那么在100个吸烟的人中必有99人患有肺癌.
的前提下认为吸烟与患肺癌有关系,那么在100个吸烟的人中必有99人患有肺癌.
B. 由独立性检验可知,在犯错误的概率不超过![]() 的前提下认为吸烟与患肺癌有关系时,我们说某人吸烟,那么他有
的前提下认为吸烟与患肺癌有关系时,我们说某人吸烟,那么他有![]() 的可能患有肺癌.
的可能患有肺癌.
C. 若从统计量中求出在犯错误的概率不超过![]() 的前提下认为吸烟与患肺癌有关系,是指有
的前提下认为吸烟与患肺癌有关系,是指有![]() 的可能性使得判断出现错误.
的可能性使得判断出现错误.
D. 以上三种说法都不正确.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥曲线 (
(![]() 是参数)和定点
是参数)和定点![]() ,
,![]() 、
、![]() 是圆锥曲线的左、右焦点.
是圆锥曲线的左、右焦点.
(1)求经过点![]() 且垂直于直线
且垂直于直线![]() 的直线
的直线![]() 的参数方程;
的参数方程;
(2)以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,求直线
轴的正半轴为极轴建立极坐标系,求直线![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com