Question

如图，在四棱柱ABCD-A₁B₁C₁D₁中，D₁D⊥底面ABCD，底面ABCD是正方形，且AB=1，D₁D=．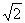

（1）求直线D₁B与平面ABCD所成角的大小；

（2）求证：AC⊥平面BB₁D₁D．

 

Answer 1

【答案】

（1）45º；（2）利用线线垂直证明线面垂直

【解析】

试题分析：（1）因为D₁D⊥面ABCD，所以BD为直线B D₁在平面ABCD内的射影，

所以∠D₁BD为直线D₁B与平面ABCD所成的角，    2分

又因为AB=1，所以BD=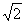，在Rt△D₁DB中，，

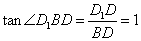所以∠D₁BD=45º，所以直线D₁B与平面ABCD所成的角为45º；    4分

（2）明：因为D₁D⊥面ABCD，AC在平面ABCD内，所以D₁D⊥AC，

又底面ABCD为正方形，所以AC⊥BD， 6分

因为BD与D₁D是平面BB₁D₁D内的两条相交直线，

所以AC⊥平面BB₁D₁D． 8分

考点：本题考查了空间中的线面关系

点评：此类问题常考查空间中平行关系与垂直关系的证明以及空间角、几何体体积的计算，这是立体几何的重点内容.证明的关键是熟练掌握并灵活运用相关的判定定理与性质定理