
【题目】已知 ![]() 函数
函数 ![]() 在区间
在区间 ![]() 上有1个零点;
上有1个零点; ![]() 函数
函数 ![]() 图象与
图象与 ![]() 轴交于不同的两点.若“
轴交于不同的两点.若“ ![]() ”是假命题,“
”是假命题,“ ![]() ”是真命题,求实数
”是真命题,求实数 ![]() 的取值范围.
的取值范围.
【答案】解:对于 ![]() 设
设 ![]() .
.
该二次函数图象开向上,对称轴为直线 ![]() ,
,
所以 ![]() ,所以
,所以 ![]() ;
;
对于 ![]() 函数
函数 ![]() 与
与 ![]() 轴交于不同的两点,
轴交于不同的两点,
所以 ![]() ,即
,即 ![]() ,
,
解得 ![]() 或
或 ![]() .
.
因为“ ![]() ”是假命题,“
”是假命题,“ ![]() ”是真命题,所以
”是真命题,所以 ![]() 一真一假.
一真一假.
①当 ![]() 真
真 ![]() 假时,有
假时,有 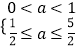 ,所以
,所以 ![]() ;
;
②当 ![]() 假
假 ![]() 真时,有
真时,有 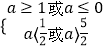 ,所以
,所以 ![]() 或
或 ![]() .
.
所以实数 ![]() 的取值范围是
的取值范围是 ![]() .
.
【解析】对于命题p,二次函数的对称轴正好在区间的左端点处,则函数在区间中是增函数,要使函数有一个零点,则端点处函数值左负右正,求出a的范围;对于命题q,二次函数与x轴有两个交点,则判别式大于0,求出a的范围。由“ p ∧ q ”是假命题,“ p ∨ q ”是真命题,则p和q一真一假,分成p真q假和p假q真求出a的范围.


科目:高中数学 来源: 题型:
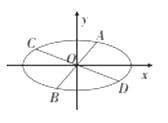
【题目】椭圆 ![]() 的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条线段,称为该直径的共轭直径,已知椭圆的方程为
的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条线段,称为该直径的共轭直径,已知椭圆的方程为 ![]() .
.
(1)若一条直径的斜率为 ![]() ,求该直径的共轭直径所在的直线方程;
,求该直径的共轭直径所在的直线方程;
(2)若椭圆的两条共轭直径为 ![]() 和
和 ![]() ,它们的斜率分别为
,它们的斜率分别为 ![]() ,证明:四边形
,证明:四边形 ![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)指出![]() 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;
(3)说明此函数图象可由![]() 的图象经怎样的变换得到.
的图象经怎样的变换得到.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一块半径为![]() 的正常数)的半圆形空地,开发商计划征地建一个矩形的游泳池
的正常数)的半圆形空地,开发商计划征地建一个矩形的游泳池![]() 和其附属设施,附属设施占地形状是等腰
和其附属设施,附属设施占地形状是等腰![]() ,其中
,其中![]() 为圆心,
为圆心, ![]() 在圆的直径上,
在圆的直径上, ![]() 在半圆周上,如图.
在半圆周上,如图.
(1)设![]() ,征地面积为
,征地面积为![]() ,求
,求![]() 的表达式,并写出定义域;
的表达式,并写出定义域;
(2)当![]() 满足
满足![]() 取得最大值时,开发效果最佳,求出开发效果最佳的角
取得最大值时,开发效果最佳,求出开发效果最佳的角![]() 的值,
的值,
求出![]() 的最大值.
的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (e为自然对数的底).若函数g(x)=f(x)﹣kx恰好有两个零点,则实数k的取值范围是( )
(e为自然对数的底).若函数g(x)=f(x)﹣kx恰好有两个零点,则实数k的取值范围是( )
A.(1,e)
B.(e,10]
C.(1,10]
D.(10,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() .
.
(1)求圆心![]() 的轨迹方程;
的轨迹方程;
(2)若![]() ,求直线
,求直线![]() 被圆
被圆![]() 所截得弦长的最大值;
所截得弦长的最大值;
(3)若直线![]() 是圆心
是圆心![]() 下方的切线,当
下方的切线,当![]() 在
在![]() 上变化时,求
上变化时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com