
【题目】如图,在三棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是以
是以![]() 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,![]() ,
,![]() 是线段
是线段![]() 上一点.
上一点.
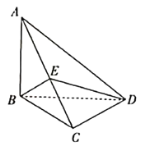
(1)若![]() 为
为![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(2)是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,请指出点
?若存在,请指出点![]() 的位置,并加以证明;若不存在,请说明理由.
的位置,并加以证明;若不存在,请说明理由.
【答案】(1)![]() (2)存在,点
(2)存在,点![]() 的坐标为
的坐标为![]() .证明见解析
.证明见解析
【解析】
以B为原点建立空间直角坐标系,(1)求出平面BDE的法向量,直线AC的方向向量,求出向量夹角的余弦值的绝对值即为直线![]() 与平面
与平面![]() 所成角的正弦值;(2)先假设结论成立,分别求出平面
所成角的正弦值;(2)先假设结论成立,分别求出平面![]() 平面
平面![]() 的法向量,由平面
的法向量,由平面![]() 平面
平面![]() 可知两法向量的数量积为0,即可求解点E的位置.
可知两法向量的数量积为0,即可求解点E的位置.
解:不妨设![]() ,在平面
,在平面![]() 中作
中作![]() ,以
,以![]() ,
,![]() ,
,![]() 所在的直线为
所在的直线为![]() ,
,![]() ,
,![]() 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)因为点![]() 是
是![]() 的中点,
的中点,
所以点![]() 的坐标为
的坐标为![]() .
.
所以![]() ,
,![]() ,
,![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则
即
取![]() ,则
,则![]() ,所以平面
,所以平面![]() 的一个法向量为
的一个法向量为![]() .
.
所以
 ,
,
所以直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.
(2)假设存在点![]() 使得平面
使得平面![]() 平面
平面![]() ,设
,设![]() .
.
显然![]() ,
,![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则 即
即
取![]() ,则
,则![]() ,
,![]() ,所以平面
,所以平面![]() 的一个法向量为
的一个法向量为![]() .
.
因为![]() ,所以点
,所以点![]() 的坐标为
的坐标为![]() .
.
所以![]() ,
,![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则 即
即
取![]() ,则
,则![]() ,所以平面
,所以平面![]() 的一个法向量为
的一个法向量为![]() .
.
因为平面![]() 平面
平面![]() ,所以
,所以![]() ,即
,即![]() ,
,![]() ,解得
,解得![]() .
.
所以![]() 的值为2,即当
的值为2,即当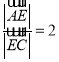 时,平面
时,平面![]() 平面
平面![]() .
.


科目:高中数学 来源: 题型:
【题目】某单位年会进行抽奖活动,在抽奖箱里装有![]() 张印有“一等奖”的卡片,
张印有“一等奖”的卡片, ![]() 张印
张印
有“二等奖”的卡片, 3张印有“新年快乐”的卡片,抽中“一等奖”获奖![]() 元, 抽中“二等奖”获奖
元, 抽中“二等奖”获奖![]() 元,抽中“新年快乐”无奖金.
元,抽中“新年快乐”无奖金.
(1)单位员工小张参加抽奖活动,每次随机抽取一张卡片,抽取后不放回.假如小张一定要将所有获奖卡片全部抽完才停止. 记![]() 表示“小张恰好抽奖
表示“小张恰好抽奖![]() 次停止活动”,求
次停止活动”,求![]() 的值;
的值;
(2)若单位员工小王参加抽奖活动,一次随机抽取![]() 张卡片.
张卡片.
①![]() 记
记![]() 表示“小王参加抽奖活动中奖”,求
表示“小王参加抽奖活动中奖”,求![]() 的值;
的值;
②设![]() 表示“小王参加抽奖活动所获奖金数(单位:元)”,求
表示“小王参加抽奖活动所获奖金数(单位:元)”,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=![]() 若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式。
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当m>0时,若对于区间[1,2]上的任意两个实数x1,x2,且x1<x2,都有![]() ,成立,求m的最大值.
,成立,求m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的是某池塘中的浮萍蔓延的面积![]() 与时间
与时间![]() 月)的关系
月)的关系![]() 有以下叙述:
有以下叙述:
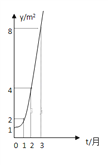
①这个指数函数的底数是2;
②第5个月时,浮萍的面积就会超过![]()
③浮萍从![]() 蔓延到
蔓延到![]() 需要经过1.5个月;
需要经过1.5个月;
④浮萍每个月增加的面积都相等;
⑤若浮萍蔓延到![]() 所经过的时间分别为
所经过的时间分别为![]() 则
则![]() .其中正确的是
.其中正确的是
A. ①② B. ①②③④ C. ②③④⑤ D. ①②⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解社会对学校办学质量的满意程度,某学校决定用分层抽样的方法从高中三个年级的家长委员会中共抽取![]() 人进行问卷调查,已知高一、高二、高三、的家长委员会分别有
人进行问卷调查,已知高一、高二、高三、的家长委员会分别有![]() 人,
人,![]() 人,
人,![]() 人.
人.
![]() 求从三个年级的家长委员会分别应抽到的家长人数;
求从三个年级的家长委员会分别应抽到的家长人数;
![]() 若从抽到的
若从抽到的![]() 人中随机抽取
人中随机抽取![]() 人进行调查结果的对比,求这
人进行调查结果的对比,求这![]() 人中至少有一人是高三学生家长的概率.
人中至少有一人是高三学生家长的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四大名著是中国文学史上的经典作品,是世界宝贵的文化遗产.某学校举行的“文学名著阅读月”活动中,甲、乙、丙、丁、戊五名同学相约去学校图书室借阅四大名著《红楼梦》、《三国演义》、《水浒传》、《西游记》(每种名著均有若干本),要求每人只借阅一本名著,每种名著均有人借阅,且甲只借阅《三国演义》,则不同的借阅方案种数为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com