
【题目】某单位建造一间地面面积为12 m2的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度x不得超过a m,房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2,屋顶和地面的造价费用合计为5800元,如果墙高为3 m,且不计房屋背面的费用.当侧面的长度为多少时,总造价最低?最低总造价是多少?
【答案】若a≥4,当x=4时,有最小值13000元;
若a<4,当x=a时,有最小值为900(a+![]() )+5800元
)+5800元
【解析】
试题分析:已知中地面面积为12m2,我们可得xy=12有![]() ,根据房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2,屋顶的造价共5200元,结合墙高为3m,我们可以构造房屋总造价的函数解析式,利用基本不等式或导数即可求出函数的最小值,进而得到答案
,根据房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2,屋顶的造价共5200元,结合墙高为3m,我们可以构造房屋总造价的函数解析式,利用基本不等式或导数即可求出函数的最小值,进而得到答案
试题解析:用长度x表示出造价,利用基本不等式求最值即可,还应注意定义域0<x≤a,函数取最小值时的x是否在定义域内,若不在定义域内,不能用不等式求最值,可以考虑单调性.
试题解析:由题意可得,造价y=3(2x×150+![]() ×400)+5800=900(x+
×400)+5800=900(x+![]() )+5800(0<x≤a).
)+5800(0<x≤a).
则y=900(x+![]() )+5800≥900×2
)+5800≥900×2![]() +5800
+5800
=13000(当且仅当x=![]() ,即x=4时取等号).
,即x=4时取等号).
若a≥4,x=4时,有最小值13000.
若a<4,任取x1、x2∈(0,a]且x1<x2,
y1-y2=900(x1+![]() )+5800-900(x2+
)+5800-900(x2+![]() )-5800
)-5800
=900[(x1-x2)+16(![]() -
-![]() )]
)]
=![]() .
.
因为0<x1<x2≤a,所以x1-x2<0,x1x2<a2<16,
所以y1-y2>0,所以y=900(x+![]() )+5800在(0,a]上是减函数,
)+5800在(0,a]上是减函数,
所以当x=a时,y有最小值900(a+![]() )+5800.
)+5800.
综上,若a≥4,当x=4时,有最小值13000元;若a<4,当x=a时,有最小值为900(a+![]() )+5800元.
)+5800元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】下列说法错误的是 ( )
A. 多面体至少有四个面
B. 九棱柱有9条侧棱,9个侧面,侧面为平行四边形
C. 长方体、正方体都是棱柱
D. 三棱柱的侧面为三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了比较两种治疗失眠症的药(分别称为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者在服用一段时间后,记录他们日平均增加的睡眠时间(单位:h),试验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:

服用B药的20位患者日平均增加的睡眠时间:

(Ⅰ)分别计算两组数据的平均数,从计算结果看,哪种药的疗效更好?
(Ⅱ)根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在
,若存在![]() ,使
,使![]() 成立,则称
成立,则称![]() 为
为![]() 的
的
不动点.已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的不动点;
的不动点;
(2)若对任意实数![]() ,函数
,函数![]() 恒有两个相异的不动点,求
恒有两个相异的不动点,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若f(x)的两个不动点为![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)对一切实数x,y均有f(x+y)-f(y)=(x+2y+1)x成立,且f(1)=0.
(1)求f(0);
(2)求f(x);
(3)当0<x<2时不等式f(x)>ax-5恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学联盟举行了一次“盟校质量调研考试”活动.为了解本次考试学生的某学科成绩情况,从中抽取部分学生的分数(满分为100分,得分取正整数,抽取学生的分数均在![]() 之内)作为样本(样本容量为n)进行统计.按照
之内)作为样本(样本容量为n)进行统计.按照![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(茎叶图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(茎叶图中仅列出了得分在![]() ,
,![]() 的数据).
的数据).
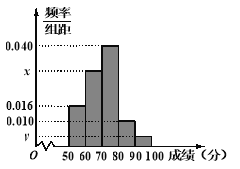
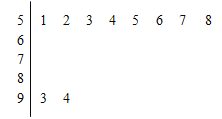
(Ⅰ)求样本容量n和频率分布直方图中的x、y的值;
(Ⅱ)在选取的样本中,从成绩在80分以上(含80分)的学生中随机抽取2名学生参加“省级学科基础知识竞赛”,求所抽取的2名学生中恰有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
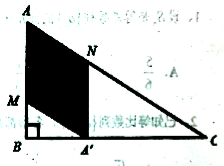
【题目】如图,某小区准备将一块闲置的直角三角形(其中![]() )土地开发成公共绿地,设计时,要求绿地部分(图中阴影部分)有公共绿地走道
)土地开发成公共绿地,设计时,要求绿地部分(图中阴影部分)有公共绿地走道![]() ,且两边是两个关于走道
,且两边是两个关于走道![]() 对称的三角形(
对称的三角形(![]() 和
和![]() ),现考虑方便和绿地最大化原则,要求
),现考虑方便和绿地最大化原则,要求![]() 点与
点与![]() 点不重合,
点不重合,![]() 点落在边
点落在边![]() 上,设
上,设![]() .
.
(1)若![]() ,绿地“最美”,求最美绿地的面积;
,绿地“最美”,求最美绿地的面积;
(2)为方便小区居民行走,设计时要求![]() 最短,求此时公共绿地走道
最短,求此时公共绿地走道![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com