分析:(I)连接CD
1,由直四棱柱的性质,可得A
1D
1BC是平行四边形,从而CD
1∥A
1B,再用三角形中位线定理证出EF∥CD
1,所以EF∥A
1B,最后用线面平行的判定定理,可证出EF∥平面A
1BD;
(II)连接AC与BD相交于点O,连接A
1O,EO.利用线面垂直的判定与性质可证出A
1O⊥BD、EO⊥BD,从而∠A
1OE就是二面角
A
1-BD-E的平面角.因此要使A
1-BD-E为直二面角,即∠A
1OE=90°,由平几知识可得△A
1AO~△OCE,利用对应线段成比例结合已知条件,可得当CE的长度为
时,二面角A
1-BD-E为直二面角.
解答:解:(I)连接CD
1,
∵直四棱柱ABCD-A
1B
1C
1D
1中,A
1D
1∥B
1C
1,A
1D
1=B
1C
1且B
1C
1∥BC,B
1C
1=BC
∴四边形A
1D
1BC是平行四边形,可得CD
1∥A
1B
∵△C
1CD
1中,EF是中位线,∴EF∥CD
1
∴EF∥A
1B-----(3分)
∵EF?面ABB
1A
1,A
1B⊆面ABB
1A
1∴EF∥平面A
1BD;…(6分)
(II)连接AC与BD相交于点O,连接A
1O,EO
∵AA
1⊥平面ABCD,BD⊆平面ABCD,∴BD⊥AA
1
∵菱形ABCD中,AC⊥BD,AC、AA
1是平面AA
1C
1C内的相交直线,
∴BD⊥平面AA
1C
1C
∵A
1O、EO⊆平面AA
1C
1C,∴A
1O⊥BD、EO⊥BD
∴∠A
1OE就是二面角A
1-BD-E的平面角,
因此,要使A
1-BD-E为直二面角,即∠A
1OE=90°,可得∠A
1OA+∠EOC=90°
∴∠OEC=∠A
1OA=90°-∠EOC,结合∠A
1AO=∠OCE=90°,得△A
1AO~△OCE.
设CE=x,所以
=
,…(*)
∵四边形ABCD是∠DAB=60°的菱形,AB=2
∴AO=OC=
AC=
,
又因为AA
1=4,代入(*)可得
=,解之得
x=∴当CE的长度为
时,二面角A
1-BD-E为直二面角.…(12分)
点评:本题给出底面为菱形的直四棱柱,证明直线与平面平行并探求了平面与平面成直角的问题,着重考查了线面平行的判定和面面垂直的定义,以及二面角的平面角求法等知识,属于中档题.

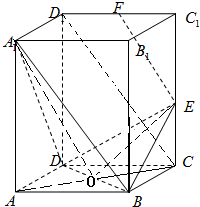
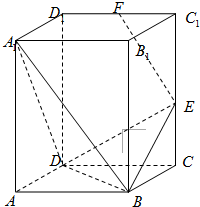 如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是∠DAB=60°的菱形,AA1=4,AB=2,点E在棱CC1上,点F是棱C1D1的中点;
如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是∠DAB=60°的菱形,AA1=4,AB=2,点E在棱CC1上,点F是棱C1D1的中点;


 如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2.
如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2. 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8. (2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点.
(2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点. 如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.