
已知向量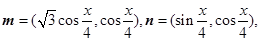 函数
函数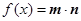 .
.
(1)求函数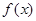 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;
(2)在锐角三角形ABC中,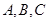 的对边分别是
的对边分别是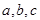 ,且满足
,且满足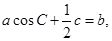 求
求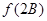 的取值范围.
的取值范围.
(1)
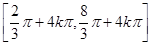 ,
, ;(2)
;(2)
【解析】
试题分析:(1)首先利用向量的坐标运算和两角和差公式求出函数 的表达式
的表达式 ,然后再根据三角函数的周期公式求出周期,由正弦函数的单调性可得
,然后再根据三角函数的周期公式求出周期,由正弦函数的单调性可得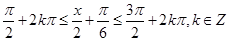 ,解出x,即得所求的单调减区间
,解出x,即得所求的单调减区间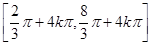 ,
, .(2)利用正弦公式把已知等式转化为角的三角函数式,再利用两角和差公式,把和角展开,整理可得sinC=2cosAsinC,即1=2cosA.得
.(2)利用正弦公式把已知等式转化为角的三角函数式,再利用两角和差公式,把和角展开,整理可得sinC=2cosAsinC,即1=2cosA.得 ,在根据三角形的内角和定理和B是锐角,求出角B的取值范围为
,在根据三角形的内角和定理和B是锐角,求出角B的取值范围为 ,即
,即 ,可得
,可得 ,所以
,所以 =
=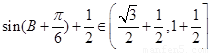 .
.
试题解析:解:(1) 3分
3分
函数 的最小正周期为T
的最小正周期为T 4分
4分
函数 的单调递减区间为
的单调递减区间为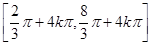 ,
, 。 6分
。 6分
(2)由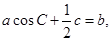 得
得 8分
8分
因为B为锐角,故有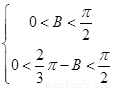 ,得
,得 10分
10分
所以 11分
11分
所以 的取值范围是
的取值范围是 . 12分
. 12分
考点:1.正弦定理;2.两角和差公式;3.正弦函数的性质.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
| 3 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| 3 |
| 1 |
| 2 |
| m |
| n |
| m |
| 3 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| 3 |
| 1 |
| 2 |
| a |
| b |
| a |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年宁夏省高三上学期第四次月考理科数学试卷(解析版) 题型:解答题
已知向量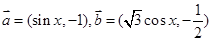 ,函数
,函数 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)已知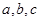 分别为
分别为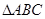 内角
内角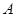 、
、 、
、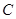 的对边, 其中
的对边, 其中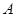 为锐角,
为锐角, 且
且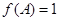 ,求
,求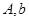 和
和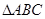 的面积
的面积 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com