练习册

  • 练习册
  • 试题
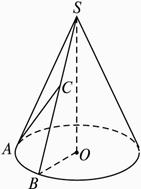
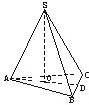    精英家教网 > 高中数学 > 题目详情
    如图2-2-2,设SA、SB是圆锥SO的两条母线,O是底面圆心,C是SB上一点,求证:AC与平面SOB不垂直.

    图2－2－2

    证明:假设AC⊥平面SOB,?

    ∵直线SO在平面SOB内,?

    ∴SO⊥AC.?

    ∵SO⊥底面圆O,

    ∴SO⊥AB.?

    ∴SO⊥平面SAB.?

    ∴平面SAB∥底面圆O.?

    这显然出现矛盾,∴假设不成立,?

    即AC与平面SOB不垂直.

    点评:否定性地问题常用反证法.例如证明异面直线,可以假设共面,再把假设作为已知条件推导出矛盾.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图，设三棱锥S-ABC的三个侧棱与底面ABC所成的角都是60°，又∠BAC=60°，且SA⊥BC．
    （1）求证：S-ABC为正三棱锥；
    （2）已知SA=a，求S-ABC的全面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

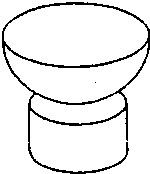    精英家教网某工艺品厂要生产如图所示的一种工艺品，该工艺品由一个圆柱和一个半球组成，要求半球的半径和圆柱的底面半径之比为3：2，工艺品的体积为34πcm3．设圆柱的底面直径为4x（cm），工艺品的表面积为S（cm2）．
    （1）试写出S关于x的函数关系式；
    （2）怎样设计才能使工艺品的表面积最小？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，矩形ABCD中，AB=4，AD=3，E，F分别是边AB，BC上的点，且AE=BF=x，设五边形AEFCD的面积为s，周长为c．
    （1）分别写出s，c关于x的函数解析式，并指出它们的定义域．
    （2）分别求s，c的最小值及取最小值时x的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图放置的边长为1的正方形PABC沿x轴滚动（向右为顺时针，向左为逆时针）．设顶点p（x，y）的轨迹方程是y=f（x），则关于f（x）的最小正周期T及y=f（x）在其两个相邻零点间的图象与x轴所围区域的面积S的正确结论是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•江西）如图，|OA|=2（单位：m），OB=1（单位：m），OA与OB的夹角为
    π
    6
    ，以A为圆心，AB为半径作圆弧
    BDC
    与线段OA延长线交与点C．甲、乙两质点同时从点O出发，甲先以速度1（单位：m/s）沿线段OB行至点B，再以速度3（单位：m/s）沿圆弧
    BDC
    行至点C后停止；乙以速率2（单位：m/s）沿线段OA行至A点后停止．设t时刻甲、乙所到的两点连线与它们经过的路径所围成图形的面积为S（t）（S（0）=0），则函数y=S（t）的图象大致是（　　）

    查看答案和解析>>

    同步练习册答案