Question

(1)已知抛物线y²=2Px(P＞0),过焦点F的动直线l交抛物线于A,B两点,O为坐标原点,求证:·为定值;

(2)由(1)可知:过抛物线的焦点F的动直线l交抛物线于A,B两点,存在定点P,使得·为定值.请写出关于椭圆的类似结论,并给出证明.

Answer 1

(1)证法一:若直线l垂直于x轴,则A(,p),B(,-p).

·=()²-p²=-.                                                                              ?

若直线l不垂直于x轴,设其方程为y=k(x-),A(x₁,y₁),B(x₂,y₂),?

由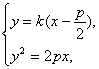得k²x²-p(2+k²)x+k²=0.?

∴x₁+x₂=,x₁x₂=.                                                                                 ?

∴·=x₁x₂+y₁y₂=x₁x₂+k²(x₁-)(x₂-)??

=(1+k²)x₁x₂-k²(x₁+x₂)+?

=(1+k²)-·+=-.?

综上,·=-为定值.                                                                          ?

证法二:设直线l的方程为x=my+,A(x₁,y₁),B(x₂,y₂).                                        ?

由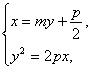得y²-2pmy-p²=0.?

∴y₁+y₂=2pm,y₁y₂=-p².                                                                                             ?

∴·=x₁x₂+y₁y₂=(my₁+)(my₂+)+y₁y₂?

=(1+m²)y₁y₂+my₁+y₂)+ ?

=(1+m²)(-p²)-·2pm=-.?

∴·=-为定值.                                                                               ?

(2)解:关于椭圆有类似的结论:过椭圆=1(A＞B＞0)的一个焦点F的动直线l交椭圆于A,B两点,存在定点P,使·为定值.                                                           ?

证明:不妨设直线l过椭圆=1的右焦点F(c,0)(其中c=).

若直线l不垂直于x轴,则设其方程为y=k(x-c),A(x₁,y₁),B(x₂,y₂).?

由得(A²k²+B²)x²-2A²CK²x+(A²c²k²-A²B²)=0.?

所以x₁+x₂=,x₁x₂=.                                                          ?

由对称性可知,设点P在x轴上,其坐标为(M,0).?

所以·=(x₁-M)(x₂-M)+y₁y₂?

=(1+k²)x₁x₂-(M+CK²)(x₁+x₂)+?M²+c²k²??

=(1+k²)-(M+CK²)+M²+c²k²?

=.?

要使·为定值,只要A⁴-A²B²-B⁴+A²M²-2A²cM=A²(M²-A²)?,

即M===.?

此时·=M²-A²==.                                      ?

若直线l垂直于x轴,则其方程为x=c,A(c,),B(c,-).?

取点P(,0),?

有·=［-c］²-=.                                       ?

综上,过焦点F(c,0)的任意直线l交椭圆于A,B两点,存在定点P(,0),

使·=为定值.